【题目】如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.

参考答案:
【答案】(1)PN与⊙O相切.证明见解析;(2)成立.证明见解析;(3)![]()
【解析】试题分析:(1)根据切线的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA进而求出即可;
(2)根据已知得出∠PNM+∠ONA=90°,进而得出∠PNO=180°-90°=90°即可得出答案;
(3)首先根据外角的性质得出∠AON=60°进而利用扇形面积公式得出即可.
试题解析:(1)PN与⊙O相切.
证明:连接ON,

则∠ONA=∠OAN,
∵PM=PN,
∴∠PNM=∠PMN,
∵∠AMO=∠PMN,
∴∠PNM=∠AMO,
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°,
即PN与⊙O相切.
(2)成立.
证明:连接ON,
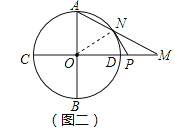
则∠ONA=∠OAN,
∵PM=PN,
∴∠PNM=∠PMN,
在Rt△AOM中,∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°-90°=90°.
即PN与⊙O相切.
(3)连接ON,

由(2)可知∠ONP=90°.
∵∠AMO=30°,PM=PN,
∴∠PNM=30°,∠OPN=60°,
∴∠PON=30°,∠AON=60°,
作NE⊥OD,垂足为点E,
则NE=ONsin30°=1×![]() =
=![]() ,
,
S阴影=S△AOC+S扇形AON-S△CON
=![]() OCOA+
OCOA+![]() ×π×12-
×π×12-![]() CONE
CONE
=![]() ×1×1+
×1×1+![]() π-
π-![]() ×1×
×1×![]()
=![]() +
+![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
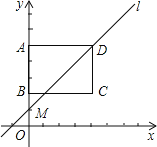
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点,且△NBD为等腰三角形,试探究:当函数y=kx+5-4k为正比例函数时,点N的个数有______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
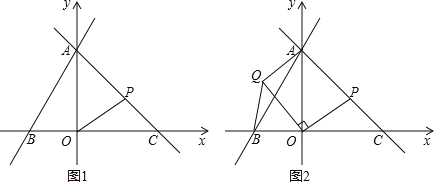
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数轴上点
 表示有理数
表示有理数 ,点
,点 表示有理数
表示有理数 ,则
,则 的中点表示的数可用公式
的中点表示的数可用公式 求得,如点
求得,如点 表示的数分别是
表示的数分别是 和
和 ,则线段
,则线段 的中点所表示的数是
的中点所表示的数是 .
.(1)如图1,点
 所表示的数是
所表示的数是 ,点
,点 所表示的数是
所表示的数是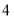 ,则
,则 的距离是_______;
的距离是_______;(2)若点
 表示的数是
表示的数是 ,线段
,线段 的中点所表示的数是
的中点所表示的数是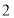 ,则点
,则点 表示的数是__________;
表示的数是__________;(3)如图1,点
 、点
、点 、点
、点 表示的数分别是
表示的数分别是 ,两个动点
,两个动点 分别从点
分别从点 和点
和点 同时出发,点
同时出发,点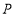 以每秒
以每秒 个单位长度的速度向右运动,点
个单位长度的速度向右运动,点 以每秒
以每秒 个单位长度的速度向右运动。
个单位长度的速度向右运动。①运动
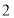 秒后点
秒后点 所表示的数是_________,运动
所表示的数是_________,运动 秒后点
秒后点 所表示的数是_______.
所表示的数是_______.②问运动几秒后,
 三个点中的一点恰好是连接另外两点的线段的中点?请说明理由.
三个点中的一点恰好是连接另外两点的线段的中点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线y=﹣x+2与反比例函数y=
 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=
的图象有唯一公共点,若直线y=﹣x+b与反比例函数y= 的图象有2个公共点,则b的取值范围是( )
的图象有2个公共点,则b的取值范围是( )
A. b>2 B. ﹣2<b<2 C. b>2或b<﹣2 D. b<﹣2
相关试题

