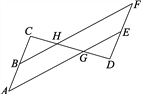
【题目】如图所示,已知B、E分别是线段AC、DF的中点,AC=DF,BF交CD于点H,AE交CD于点G,CH=HG=DG,BH=GE.
(1)填空:因为B、E分别是线段AC、DF的中点,所以CB=________AC,DE=________DF.因为AC=DF,所以CB=________.在△CBH和△DEG中,因为CB=________,CH=________,BH=________EG,所以________≌________(SSS).
(2)除了(1)中的全等三角形外,请你再写出另外一对全等三角形,并说明理由.
参考答案:
【答案】(1) ![]() ,
, ![]() ,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
【解析】试题分析:(1)因为B是AC的中点, ![]() 同理
同理![]() 因为AC=DF,由上知
因为AC=DF,由上知![]() 根据上面求得:
根据上面求得: ![]() 即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
(2)根据题中条件分析,再用SAS来证明即可
试题解析:(1)因为B是AC的中点, ![]() 同理
同理![]()
因为AC=DF,由上知![]() 根据上面求得:
根据上面求得:
![]() 即可得△CBH≌△DEG.
即可得△CBH≌△DEG.
故答案为: ![]() ,
, ![]() ,DE,DE,DG,△CBH,△DEG.
,DE,DE,DG,△CBH,△DEG.
(2)△AGC≌△FHD.
理由:因为△CBH≌△DEG,
所以∠C=∠D.因为CH=HG=DG,
所以CG=DH.
在△AGC和△FHD中,
因为AC=FD,∠C=∠D,CG=DH,
所以△AGC≌△FHD(SAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC是钝角,画出:
(1)∠BAC的平分线;
(2)AC边上的中线;
(3)AC边上的高;
(4)AB边上的高.

-
科目: 来源: 题型:
查看答案和解析>>【题目】 计算(x3y)2的结果是( )
A.x3y2B.x6yC.x5y2D.x6y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-3,0)在___轴上,点B(-2,-3)在第___象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】武汉市今年元月某天的最高气温是8℃,最低气温是﹣2℃,则这一天的温差是( )
A.8℃
B.﹣6℃
C.6℃
D.10℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
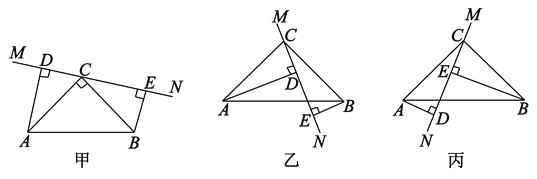
(1)当直线MN绕点C旋转到图甲的位置时,试说明:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,试说明:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(
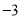 ,0)、(0,4),抛物线
,0)、(0,4),抛物线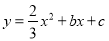 经过B点,且顶点在直线
经过B点,且顶点在直线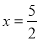 上.
上.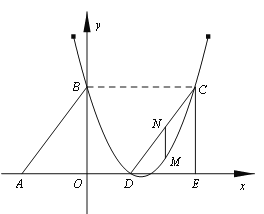
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
相关试题

