【题目】如图,已知∠AOB=∠BOC=∠COD,下列结论中错误的是( )

A. OB、OC分别平分![]() 、
、![]()
B. ![]()
C. ![]()
D. ![]()
参考答案:
【答案】C
【解析】
根据角平分线的定义和角的和差逐一进行判断即可.
A、∵∠AOB=∠BOC=∠COD,
∴OB、OC分别平分∠AOC、∠BOD,故正确;
B、∵∠AOB=∠BOC=∠COD,
∴∠AOC=∠BOD,
∵∠AOD=∠AOB+∠BOD,
∴∠AOD=∠AOB+∠AOC,故正确;
C、∵∠BOC═∠AOC-∠AOB,
∵∠AOB=∠BOC=∠COD,
∴∠AOC=![]() ∠AOD,
∠AOD,
∴∠BOC=![]() ∠AOD-∠AOB,故错误;
∠AOD-∠AOB,故错误;
D、∵∠AOB=∠COD,
∴∠COD=∠AOD-∠BOC-∠AOB,
∴2∠COD=∠AOD-∠BOC,
∴∠COD=![]() (∠AOD-∠BOC),故正确,
(∠AOD-∠BOC),故正确,
故选C.
-
科目: 来源: 题型:
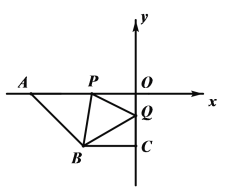
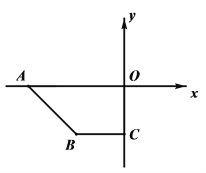
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足
 ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使
 ,求出点P的坐标;
,求出点P的坐标;(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现】:如图1,在正三角形ABC中,在AB,AC边上分别取点M,N,BM=AN,连接BN,CM,相交于点O,求∠α
易得:△ABN≌△BCN,则∠1=∠2
∵∠α是△BOC的外角,∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】:在正n边形中,对相邻的两边实施同样的操作…
(1)如图2,在正四边形ABCD中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(2)如图3,在正五边形ABCDE中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(3)判断:∠α可以等于160°吗?如果可以,求出对应的边数n,若不可以,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠AOC=
 ∠COB,则∠BOF=_____°.
∠COB,则∠BOF=_____°.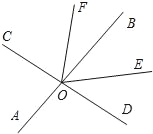
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
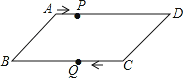
A. 4次 B. 3次 C. 2次 D. 1次
相关试题

