【题目】某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
●操作发现
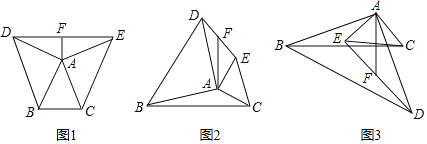
在等腰△ABC中,AB=AC,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE,其中F是DE的中点,连接AF,则下列结论正确的是 (填序号即可)
①AF=![]() BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
●数学思考
在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE,其中F是DE的中点,连接AF,则AF和BC有怎样的数量和位置关系?请给出证明过程
●类比探索
在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE,其中F是DE的中点,连接AF,试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
参考答案:
【答案】操作发现:①②③④;数学思考:AF=![]() BC,AF⊥BC,理由见解析;类比探索:AF和BC的数量和位置关系不发生改变,理由见解析
BC,AF⊥BC,理由见解析;类比探索:AF和BC的数量和位置关系不发生改变,理由见解析
【解析】
操作发现:
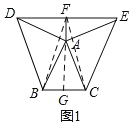
如图1,延长FA交BC于G,连接BF、CF.证明△FBA≌△FCA(SAS),得FB=FC,根据线段垂直平分线的逆定理可得FG是BC的垂直平分线,得②正确;
证明∠AFD≌△BGA(AAS),则AF=BG![]() BC,得①正确;
BC,得①正确;
根据内错角相等两直线平行,得④正确;
根据前面的证明可以得出整个图形是轴对称图形,故③正确,数学思考:
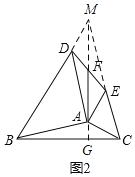
结论:AF![]() BC,AF⊥BC,如图2,作辅助线,构建平行四边形和三角形全等,证明四边形DAEM是平行四边形,得AD=EM=AB,AD∥EM,再证明△CAB≌△AEM(SAS),可得结论;
BC,AF⊥BC,如图2,作辅助线,构建平行四边形和三角形全等,证明四边形DAEM是平行四边形,得AD=EM=AB,AD∥EM,再证明△CAB≌△AEM(SAS),可得结论;
类比探索:
同理作辅助线,构建平行四边形和全等三角形,同理可得结论.
操作发现:
如图1,延长FA交BC于G.
∵△ABD和△ACE是等腰直角三角形,且∠BAD=∠CAE=90°,∴AB=AD,AC=AE.
∵AB=AC,∴AD=AE.
∵F是DE的中点,∴AF⊥DE,∠DAF=∠EAF,∴∠BAF=∠CAF.
∵AB=AC,AF=AF,∴△FBA≌△FCA(SAS),∴FB=FC,∴FG是BC的垂直平分线,即FG⊥BC,AF⊥BC,故②正确;
∵∠AGB=∠AFD=90°,∠BAG=∠FDA,∴∠AFD≌△BGA(AAS),∴AF=BG![]() BC,故①正确;
BC,故①正确;
∵∠AFD=∠AGC=90°,∴DE∥BC,故④正确;
根据前面的证明可以得出将图形1,沿FG对折左右两部分能完全重合,∴整个图形是轴对称图形,故③正确,结论正确的有:①②③④.
故答案为:①②③④;
数学思考:
结论:AF![]() BC,AF⊥BC,理由是:
BC,AF⊥BC,理由是:
如图2,延长AF至M,使FM=AF,连接DM、EM,延长FA交BC于G.
∵DF=EF,∴四边形DAEM是平行四边形,∴AD=EM=AB,AD∥EM,∴∠DAE+∠AEM=∠DAE+∠BAC=180°,∴∠BAC=∠AEM.
∵AC=AE,∴△CAB≌△AEM(SAS),∴AM=BC=2AF,∠AME=∠CBA,即AF![]() BC.
BC.
∵AD∥EM,∴∠DAM=∠AME=∠CBA.
∵∠BAD=90°,∴∠DAM+∠BAG=90°,∴∠CBA+∠BAG=∠AGB=90°,∴AF⊥BC;
类比探索:
AF和BC的数量和位置关系不发生改变,理由是:
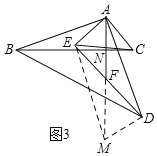
如图3,延长AF至M,使AF=FM,连接EM、DM,设AF交BC于N.
∵EF=DF,∴四边形AEMD是平行四边形,∴AE=DM=AC.
∵∠BAD+∠EAC=180°,∴∠BAC+∠EAD=180°.
∵AE∥DM,∴∠ADM+∠EAD=180°,∴∠ADM=∠BAC.
∵AB=AD,∴△ABC≌△DAM(SAS),∴AM=BC=2AF,∠DAM=∠ABC,∴AF![]() BC.
BC.
∵∠DAM+∠BAF=∠ABC+∠BAF=90°,∴∠ANB=90°,∴AF⊥BC.
-
科目: 来源: 题型:
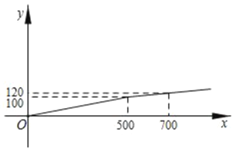
查看答案和解析>>【题目】改革开放40年来,中国已经成为领先世界的基建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动,BC∥HG,AE⊥BC,垂足为点E,AE的延长线交HG于点G,经测量,∠ABD=11°,∠ADE=26°,∠ACE=31°,BC=20m,EG=0.6m.
(1)求线段AG的长度;
(2)连接AF,当线段AF⊥AC时,求点F和点G之间的距离.
(所有结果精确到0.1m.参考数据:tan11°≈0.19,tan26°≈0.49,tan31°≈0.60)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校一课外小组准备进行“绿色环保”的宣传活动,需要印刷一批宣传单,学校附近有甲、乙两家印刷社,甲印刷社收费y(元)与印数x(张)的函数关系是:y=0.15x;乙印刷社收费y(元)与印数x(张)的函数关系如图所示:
(1)写出乙印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两印刷社打印了相同数量的宣传单共用去70元,则共打印多少张宣传单?
(3)活动结束后,市民反映良好,兴趣小组决定再加印1500张宣传单,若在甲、乙印刷社中选一家,兴趣小组应选择哪家印刷社比较划算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线P:
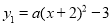 与抛物线Q:
与抛物线Q: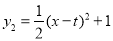 在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.(1)求a的值及点B的坐标;
(2)当抛物线Q经过点A时
①求抛物线Q的解析式;
②设直线l与抛物线Q的另一交点为C,求
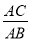 的值.
的值.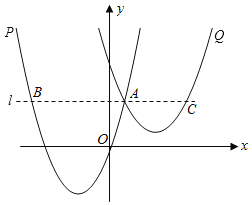
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学进行长跑训练,甲和乙所跑的路程S(单位:米)与所用时间t(单位:秒)之间的函数图象分别为线段OA和折线OBCD.则下列说法正确的是( )
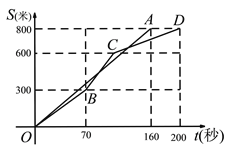
A. 两人从起跑线同时出发,同时到达终点
B. 跑步过程中,两人相遇一次
C. 起跑后160秒时,甲、乙两人相距最远
D. 乙在跑前300米时,速度最慢
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
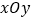 中,直线
中,直线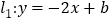 与
与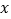 轴,
轴,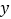 轴分别交于点
轴分别交于点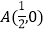 ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为 .
.(1)求反比例函数的表达式;
(2)设直线
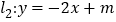 与
与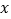
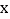 轴,
轴,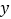 轴分别交于点C,D,且
轴分别交于点C,D,且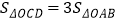 ,直接写出
,直接写出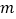 的值 .
的值 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.
相关试题

