【题目】如图,已知△ABC,∠ACB=90,AC=BC,点E、F在AB上,∠ECF=45,
(1)求证:△ACF∽△BEC
(2)设△ABC的面积为S,求证:AF·BE=2S

参考答案:
【答案】(1)证明见解析;
(2)证明见解析.
【解析】证明:(1) ∵ AC=BC, ∴ ∠A = ∠B
∵ ∠ACB=90, ∴ ∠A = ∠B = 45 0,
∵ ∠ECF= 45, ∴ ∠ECF = ∠B = 45,
∴ ∠ECF+∠1 = ∠B+∠1
∵ ∠BCE = ∠ECF+∠1,∠2 = ∠B+∠1;
∴ ∠BCE = ∠2,
∵ ∠A = ∠B ,AC=BC,
∴ △ACF∽△BEC。
解:(2)∵△ACF∽△BEC
∴ AC = BE,BC = AF,
∴△ABC的面积:S = ![]() AC·BC =
AC·BC = ![]() BE·AF
BE·AF
∴AF·BE=2S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(3)班的同学踊跃为“雅安芦山地震”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但生活委员不小心把墨水滴在统计表上,部分数据看不清楚。
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象如图,则k、b的符号是( )
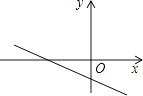
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】五边形的内角和是°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣2x+4的图象与x轴交点坐标是 , 与y轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .
相关试题

