【题目】三角形ABC三个顶点的坐标分别是A(-4,-1),B(1,1),C(-1,4),将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A. (2,2),(3,4),(1,7) B. (-2,2),(4,3),(1,7)
C. (-2,2),(3,4),(1,7) D. (2,-2),(3,3),(1,7)
参考答案:
【答案】C
【解析】已知A(-4,-1),B(1,1),C(-1,4),将△ABC向右平移2个单位长度,再向上平移3个单位长度,所得坐标是:(-4+2,-1+3),(1+2,1+3),(-1+2,4+3),即:(-2,2,)(3,4)(1,7),故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(-1,0);
⑤当1<x<4时,有y2<y1,
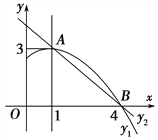
其中正确的是( ).
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
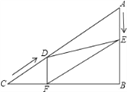
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在证明命题“一个三角形中至少有一个内角不大于60°”成立时,我们利用反证法,先假设 , 则可推出三个内角之和大于180°,这与三角形内角和定理相矛盾.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,求证:∠B<90°,用反证法证明:第一步是:假设 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在第二象限,它的横坐标与纵坐标的和是1,点P的坐标可以是________(只要写出符合条件的一个点即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P到x轴的距离是2,到y轴的距离是3,则点P 的坐标为 .
相关试题

