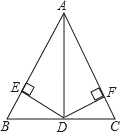
【题目】如图,在△ABC中,AD平分∠BAC交BC于D,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:AB=AC;
(2)若DC=4,∠DAC=30°,求AD的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据角平分线的性质得到DE=DF,证明Rt△BDE≌Rt△CDF,根据全等三角形的性质得到∠B=∠C,根据等腰三角形的判定定理证明;
(2)根据直角三角形的性质求出AC,根据勾股定理计算即可.
(1)证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,![]() ,
,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴AB=AC;
(2)∵AD平分∠BAC,BD=CD,
∴AD⊥BC,
∵∠DAC=30°,
∴AC=2DC=8,
∴AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来根据以上信息,解答下列问题:
(1)设租车时间为
 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数表达式;
的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC.AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)(π﹣1)0+(
 )﹣1+|5﹣
)﹣1+|5﹣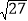 |﹣
|﹣ ;
;(2)(2
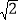 +3)2017×(2
+3)2017×(2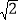 ﹣3)2018﹣4
﹣3)2018﹣4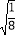 ﹣
﹣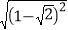 ;
;(3)
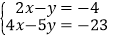 ;(4)
;(4)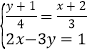 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为
 ,宽为
,宽为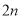 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出
 ,
, ,
, 之间的等量关系,并验证;
之间的等量关系,并验证;
(3)根据(2)题中的等量关系,解决如下问题:
①若
 ,
, ,求
,求 的值;
的值;②若
 ,
, ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:

该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
相关试题

