【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
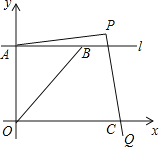
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.
参考答案:
【答案】(1)、PA=2;(2)、1:1;(3)、16.
【解析】
试题分析:(1)、根据点P与点B重合,得出PA的长度;(2)、过点P作PM⊥x轴,过点P作PN⊥y轴,根据点A的纵坐标和点B的横坐标相等得出OA=OB,根据∠OAB=90°可得∠AOB=∠ABO=45°,结合角度之间的关系得出△ANP和△CMP全等得出PA=PC,从而得到比值;(3)、根据∠ANP=∠MON=∠OMP =90°得出四边形OMPN为矩形,根据PM=PN得出四边形OMPN为正方形,根据OA=AB=3,得出OB、BP、OP的长度,根据△ANP和△CMP全等得出四边形的面积.
试题解析:(1)、∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
(2)、过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示
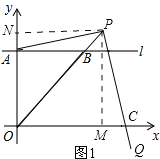
∵点A的纵坐标与点B的横坐标相等,
∴OA=AB.
∵∠OAB=90°,
∴∠AOB=∠ABO=45°
∵∠AOC=90°,
∴∠POC=45°
∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP =90°
∴∠NPM=90°
∵∠APC=90°
∴∠APN=90°﹣∠APM=∠CPM
在△ANP和△CMP中,
∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.
∴PA=PC.
∴PA:PC的值为1:1
(3)、∵∠ANP=∠MON=∠OMP =90°
∴四边形OMPN为矩形
∵PM=PN
∴四边形OMPN为正方形
∵∠OAB=90°,OA=AB=3
∴OB=![]()
∵OB:BP=3:1
∴BP=![]()
∴OP=![]()
∴![]() 正方形OMPN=
正方形OMPN=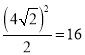
∵△ANP≌△CMP.
∴S△ANP≌S△CMP.
∴![]() 四边形AOCO=
四边形AOCO=![]() 正方形OMPN=16
正方形OMPN=16
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:0.125(a2+b2)3(a-b)2·16(-a2-b2)3(b-a)3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的第一边长是a+2b,第二边比第一边长(b - 2),第三边比第二边短5,则三角形的周长为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
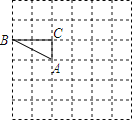
(1)画出旋转后的△AB′C′;
(2)以点C为坐标原点,线段BC、AC所在直线分别为x轴,y轴建立直角坐标系,请直接写出点B′的坐标 ;
(3)写出△ABC在旋转过程中覆盖的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(
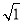 )2+1=2 S1=
)2+1=2 S1=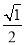 ;
;OA32=(
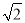 )2+1=3 S2=
)2+1=3 S2=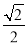 ;
;OA42=(
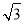 )2+1=4 S3=
)2+1=4 S3=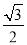 …
…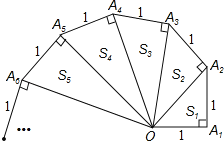
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF,相似比为3:5,△ABC的周长为6,则△DEF的周长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a3mb和 - 2a6bn+2是同类项,化简并求值:2(m2 - mn) - 3(2m2 - 3mn) - 2[m2 - (2m2 - mn+m2)] - 1.
相关试题

