【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

参考答案:
【答案】(1)(0,1)(2) y=-![]() x(x-4)=-
x(x-4)=-![]() x2+
x2+![]() x(3)满足条件的点Q有3个,分别为(3,
x(3)满足条件的点Q有3个,分别为(3, ![]() )或(2+
)或(2+![]() ,-
,- ![]() )或(2-
)或(2-![]() ,-
,- ![]() ).
).
【解析】试题分析:(1)根据抛物线勾股点的定义可以求解,(2)作PG⊥x轴,由点P的坐标求得:AG=1,PG=![]() ,由三角函数可得:
,由三角函数可得: ![]() ,可知∠PAG=60°从而求得AB=4,即B(4,0),待定系数法可求解得,(3)由
,可知∠PAG=60°从而求得AB=4,即B(4,0),待定系数法可求解得,(3)由![]() 且两个三角形同底,可知点Q到x轴的距离为
且两个三角形同底,可知点Q到x轴的距离为![]() ,即可求解.
,即可求解.
(1)抛物线y=-x2+1的勾股点的坐标为(0,1).
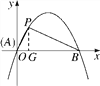
(2)如图,作PG⊥x轴于点G.∵点P的坐标为(1,![]() ),∴AG=1,PG=
),∴AG=1,PG=![]() ,∴PA=
,∴PA=![]() =
=![]() =2.∵tan∠PAB=
=2.∵tan∠PAB=![]() =
=![]() ,∴∠PAG=60°.在Rt△PAB中,AB=
,∴∠PAG=60°.在Rt△PAB中,AB=![]() =
=![]() =4,∴点B的坐标为(4,0).
=4,∴点B的坐标为(4,0).
设y=ax(x-4),将点P(1,![]() )代入得a=-
)代入得a=-![]() ,∴y=-
,∴y=-![]() x(x-4)=-
x(x-4)=-![]() x2+
x2+![]() x.
x.
(3)①当点Q在x轴上方时,由S△ABQ=S△ABP知点Q的纵坐标为![]() ,则有-
,则有-![]() x2+
x2+![]() x=
x=![]() ,解得x1=3,x2=1(不符合题意,舍去),∴点Q的坐标为(3,
,解得x1=3,x2=1(不符合题意,舍去),∴点Q的坐标为(3,![]() ).
).
②当点Q在x轴下方时,由S△ABQ=S△ABP知点Q的纵坐标为-![]() ,则有-
,则有-![]() x2+
x2+![]() x=-
x=-![]() ,解得x1=2+
,解得x1=2+![]() ,x2=2-
,x2=2-![]() ,∴点Q的坐标为(2+
,∴点Q的坐标为(2+![]() ,-
,-![]() )或(2-
)或(2-![]() ,-
,-![]() ).
).
综上所述,满足条件的点Q有3个,分别为(3,![]() )或(2+
)或(2+![]() ,-
,-![]() )或(2-
)或(2-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2)第一个数表示左右方向,第二个数表示上下方向.
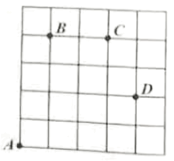
(1)图中A→C可以记为( , )
(2)图中D→ 可以记为(-4,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题

(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF.

(1)求证:DE⊥DF;
(2)如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;
(3)如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5
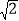 ,求AG的长.
,求AG的长. -
科目: 来源: 题型:
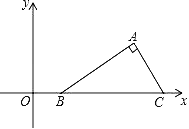
查看答案和解析>>【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
A. (﹣4,﹣2﹣
 ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+ ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+ ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
相关试题

