【题目】已知抛物线y=x2+(2m+1)x+m(m﹣3)(m为常数,﹣1≤m≤4).A(﹣m﹣1,y1),B(![]() ,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较y1,y2,y3之间的大小.
参考答案:
【答案】(1)顶点坐标(﹣![]() ,﹣
,﹣![]() );(2)k=3;(3)﹣1≤m<﹣
);(2)k=3;(3)﹣1≤m<﹣![]() 或
或![]() <m≤
<m≤![]() 时,有y2>y1=y3,﹣
时,有y2>y1=y3,﹣![]() <m<﹣
<m<﹣![]() 时,有y2<y1=y3.
时,有y2<y1=y3.
【解析】
试题分析:(1)根据顶点坐标公式表示出顶点坐标即可;(2)把两个解析式联立后得一个一元二次方程,利用△=0即可求k值;(3)首先证明y1=y3,再根据点B的位置,分类讨论,①令![]() <﹣m﹣1,求出m的范围即可判断,②令
<﹣m﹣1,求出m的范围即可判断,②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.③令
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.③令![]() >﹣m﹣1,求出m的范围即可判断,④令﹣
>﹣m﹣1,求出m的范围即可判断,④令﹣![]() ≤
≤![]() <﹣m,求出m的范围即可判断,⑤令
<﹣m,求出m的范围即可判断,⑤令![]() =﹣m,B,C重合,不合题意舍弃.⑥令
=﹣m,B,C重合,不合题意舍弃.⑥令![]() >﹣m,求出m的范围即可判断.
>﹣m,求出m的范围即可判断.
试题解析:(1)∵﹣![]() =﹣
=﹣![]() ,
,![]() =﹣
=﹣![]() ,
,
∴顶点坐标(﹣![]() ,﹣
,﹣![]() ).
).
(2)由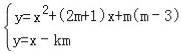 消去y得x2+2mx+(m2+km﹣3m)=0,
消去y得x2+2mx+(m2+km﹣3m)=0,
∵抛物线与x轴有且仅有一个公共点,
∴△=0,即(k﹣3)m=0,
∵无论m取何值,方程总是成立,
∴k﹣3=0,
∴k=3,
(3)PH=|﹣![]() ﹣(﹣
﹣(﹣![]() )|=|
)|=|![]() |,
|,
∵1<PH≤6,
∴当![]() >0时,有1<
>0时,有1<![]() ≤6,又﹣1≤m≤4,
≤6,又﹣1≤m≤4,
∴![]() <m≤
<m≤![]() ,
,
当![]() <0时,1<﹣
<0时,1<﹣![]() ≤6,又∵﹣1≤m≤4,
≤6,又∵﹣1≤m≤4,
∴﹣1![]() ,
,
∴﹣1≤m<﹣![]() 或
或![]() <m≤
<m≤![]() ,
,
∵A(﹣m﹣1,y1)在抛物线上,
∴y1=(﹣m﹣1)2+(2m+1)(﹣m﹣1)+m(m+3)=﹣4m,
∵C(﹣m,y3)在抛物线上,
∴y3=(﹣m)2+(2m+1)(﹣m)+m(m﹣3)=﹣4m,
∴y1=y3,
①令![]() <﹣m﹣1,则有m<﹣
<﹣m﹣1,则有m<﹣![]() ,结合﹣1≤m≤﹣
,结合﹣1≤m≤﹣![]() ,
,
∴﹣1≤m<﹣![]() ,
,
此时,在对称轴的左侧y随x的增大而减小,如图1,
∴y2>y1=y3,
即当﹣1≤m<﹣![]() 时,有y2>y1=y3.
时,有y2>y1=y3.
②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令![]() >﹣m﹣1,且
>﹣m﹣1,且![]() ≤﹣
≤﹣![]() 时,有﹣
时,有﹣![]() <m≤﹣
<m≤﹣![]() ,结合﹣1≤m<﹣
,结合﹣1≤m<﹣![]() ,
,
∴﹣![]() <m≤﹣
<m≤﹣![]() ,
,
此时,在对称轴的左侧,y随x的增大而减小,如图2,
∴y1=y3>y2,
即当﹣![]() <m≤﹣
<m≤﹣![]() 时,有y1=y3>y2,
时,有y1=y3>y2,
④令﹣![]() ≤
≤![]() <﹣m,有﹣
<﹣m,有﹣![]() ≤m<0,结合﹣1≤m<﹣
≤m<0,结合﹣1≤m<﹣![]() ,
,
∴﹣![]() ≤m<﹣
≤m<﹣![]() ,
,
此时,在对称轴的右侧y随x的增大而增大,如图3,
∴y2<y3=y1.
⑤令![]() =﹣m,B,C重合,不合题意舍弃.
=﹣m,B,C重合,不合题意舍弃.
⑥令![]() >﹣m,有m>0,结合
>﹣m,有m>0,结合![]() <m≤
<m≤![]() ,
,
∴![]() <m≤
<m≤![]() ,
,
此时,在对称轴的右侧,y随x的增大而增大,如图4,
∴y2>y3=y1,
即当![]() <m≤
<m≤![]() 时,有y2>y3=y1,
时,有y2>y3=y1,
综上所述,﹣1≤m<﹣![]() 或
或![]() <m≤
<m≤![]() 时,有y2>y1=y3,
时,有y2>y1=y3,
﹣![]() <m<﹣
<m<﹣![]() 时,有y2<y1=y3.
时,有y2<y1=y3.

-
科目: 来源: 题型:
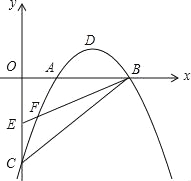
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
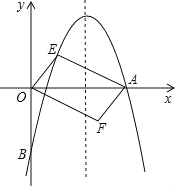
查看答案和解析>>【题目】如图,对称轴为直线x=的抛物线经过点A(6,0)和B(0,﹣4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】巴黎与北京的时间差为﹣7时(正数表示同一时刻比北京时间早的时数),如果北京时间是7月2日14:00,那么巴黎时间是( )
A. 7月2日21时 B. 7月2日7时 C. 7月1日7时 D. 7月2日5时
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.000000025=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形,上述结论中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣3)2可以看作是由抛物线y=2x2按下列何种变换得到的( )
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
相关试题

