搜索
【题目】如图，顺次连接边长为1的正方形ABCD四边的中点，得到四边形A1B1C1D1 ， 然后顺次连接四边形A1B1C1D1四边的中点，得到四边形A2B2C2D2 ， 再顺次连接四边形A2B2C2D2四边的中点，得到四边形A3B3C3D3 ， …，按此方法得到的四边形A8B8C8D8的周长为 ． 
参考答案：
【答案】
【解析】解：顺次连接正方形ABCD四边的中点得正方形A1B1C1D1 ， 则得正方形A1B1C1D1的面积为正方形ABCD面积的一半，即 
，则周长是正方形ABCD的 
； 顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2 ， 则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半，即正方形ABCD的 ，则周长是正方形ABCD的 ；
顺次连接正方形A2B2C2D2得正方形A3B3C3D3 ， 则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半，即正方形ABCD的 
，则周长是正方形ABCD的 
；
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4 ， 则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半，即正方形ABCD的 
，则周长是正方形ABCD的 ；
…
故第n个正方形周长是原来的 
，
以此类推：正方形A8B8C8D8周长是原来的 ，
∵正方形ABCD的边长为1，周长为4，
∴按此方法得到的四边形A8B8C8D8的周长为 ，
所以答案是： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了考察冰川的融化状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km的圆形考察区域，线段P1P2是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动，若经过n年，冰川的边界线P1P2移动的距离为s（km），并且s与n（n为正整数）的关系是s=
n2﹣ 
n+ 
．以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别为（﹣4，9）、（﹣13、﹣3）． 
（1）求线段P1P2所在直线对应的函数关系式；
（2）求冰川边界线移动到考察区域所需的最短时间． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），交y轴于点C，直线l过点C，且交抛物线于另一点E（点E不与点A、B重合）．
（1）求此二次函数关系式；
（2）若直线l1经过抛物线顶点D，交x轴于点F，且l1∥l，则以点C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由．
（3）若过点A作AG⊥x轴，交直线l于点G，连接OG、BE，试证明OG∥BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
问题思考：
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC、BPEF．
（1）当点P运动时，这两个正方形的面积之和是定值吗？若是，请求出；若不是，请求出这两个正方形面积之和的最小值．
（2）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
问题拓展：
（3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向点D运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．
（4）如图3，在“问题思考”中，若点M、N是线段AB上的两点，且AM=BN=1，点G、H分别是边CD、EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）32﹣|﹣2|﹣（π﹣3）0+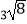
；
（2）（1+
）÷ 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形网格中小方格边长为1，请你根据所学的知识解决下面问题．
（1）求网格图中△ABC的面积．
（2）判断△ABC是什么形状？并所明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在三角形纸片ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB、AC于点E、F，连接DE、DF．求证：四边形AEDF是菱形．
相关试题
