【题目】某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
![]()
类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
册数(本) | 128 | 80 | m | 48 |
(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数;
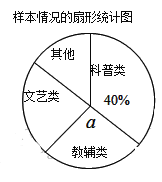
(2)该校2014年八年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本?
参考答案:
【答案】(1)64,90°;(2)1000.
【解析】试题分析:(1)首先根据科普类所占的百分比和册数求得总册数,然后相减即可求得m的值;用教辅类书籍除以总册数乘以周角即可求得其圆心角的度数;
(2)用该年级的总人数乘以教辅类的学生所占比例,即可求出该年级共借阅教辅类书籍人数.
试题解析:(1)观察扇形统计图知:科普类有128册,占40%,∴借阅总册数为128÷40%=320本,∴m=320﹣128﹣80﹣48=64;教辅类的圆心角为:360°×![]() =90°;
=90°;
(2)设全校500名学生借阅教辅类书籍x本,根据题意得: ![]() ,解得:x=1000,
,解得:x=1000,
∴八年级500名学生中估计共借阅教辅类书籍约1000本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(
 2,3),B(5,0),C(
2,3),B(5,0),C( ,
,  2).
2).①当
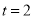 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(
 ,
,  ),其中点E是函数
),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断错误的是( )
A.有两组邻边相等的四边形是菱形B.有一角为直角的平行四边形是矩形
C.对角线互相垂直且相等的平行四边形是正方形D.矩形的对角线互相平分且相等
-
科目: 来源: 题型:
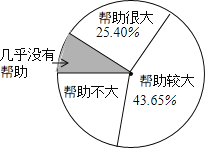
查看答案和解析>>【题目】为了解“数学思想作文对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表来表示(图、表都没制作完成).
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值.
(注:计算中涉及到的“人数”均精确到1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(x+2)(x-5)=18.
相关试题

