【题目】如图,已知反比例函数y= ![]() (k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1. 
(1)求m,k的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y= ![]() 的图象有两个不同的公共点,求实数n的取值范围.
的图象有两个不同的公共点,求实数n的取值范围.
参考答案:
【答案】
(1)解:由已知得:S△AOB= ![]() ×1×m=1,
×1×m=1,
解得:m=2,
把A(1,2)代入反比例函数解析式得:k=2
(2)解:由(1)知反比例函数解析式是y= ![]() ,
,
由题意得:  有两个不同的解,即
有两个不同的解,即 ![]() =nx+2有两个不同的解,
=nx+2有两个不同的解,
方程去分母,得:nx2+2x﹣2=0,
则△=4+8n>0,
解得:n>﹣ ![]() 且n≠0
且n≠0
【解析】(1)根据三角形的面积公式即可求得m的值;(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y= ![]() 的图象有两个不同的公共点,则方程
的图象有两个不同的公共点,则方程 ![]() =nx+2有两个不同的解,利用根的判别式即可求解.
=nx+2有两个不同的解,利用根的判别式即可求解.
-
科目: 来源: 题型:
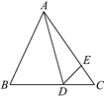
查看答案和解析>>【题目】如图,△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川省“单独两孩”政策于2014年3月20日正式开始实施,该政策的实施可能给我们的生活带来一些变化,绵阳市人口计生部门抽样调查了部分市民(每个参与调查的市民必须且只能在以下6种变化中选择一项),并将调查结果绘制成如下统计图:
种类
A
B
C
D
E
F
变化
有利于延缓社会老龄化现象
导致人口暴增
提升家庭抗风险能力
增大社会基本公共服务的压力
缓解男女比例不平衡现象
促进人口与社会、资源、环境的协调可持续发展

根据统计图,回答下列问题:
(1)参与调查的市民一共有人;
(2)参与调查的市民中选择C的人数是人;
(3)∠α=;
(4)请补全条形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,
 都是等边三角形,连接BN
都是等边三角形,连接BN  求证:
求证:  ;
; 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系 不需证明
不需证明 ;
; 如图4,当
如图4,当 时,证明:
时,证明:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足
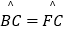 ,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点. 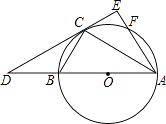
(1)求证:AE⊥DE;
(2)若tan∠CBA=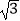 ,AE=3,求AF的长.
,AE=3,求AF的长.
相关试题

