【题目】实验探究:
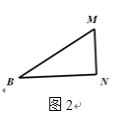
(1)如图1,对折矩形纸片ABCD,使AD与BC重合, 得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
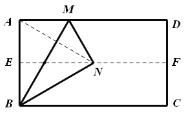
(2)将图1中的三角形纸片BMN剪下,如图2. 折叠该纸片,探究MN与BM的数量关系.写出折叠方案, 并结合方案证明你的结论.

参考答案:
【答案】(1)![]() ,证明见解析;(2)
,证明见解析;(2)![]()
【解析】
试题分析:(1)连接AN,根据折叠可以得出△ABN为等边三角形,即可求得∠MBN=30°.(2)由第一问可知三角形AMN为有一个锐角是30°的直角三角形.据此设计折叠方案:折叠三角形纸片BMN,使点N落在BM上,并使折痕经过点M,得到折痕MP,同时得到线段PO.再利用折叠和全等三角形证明结论即可.
试题解析:(1)![]()
证明:连接AN, ∵直线EF是AB的垂直平分线,点N在EF上,
∴AN=BN.
由折叠可知,BN=AB,
∴△ABN是等边三角形.
∴![]() .
.
∴![]() .
.
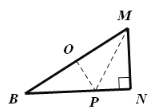
(2)![]() 折纸方案:如图,折叠三角形纸片BMN,使点N落在BM上,并使折痕经过点M,得到折痕MP,同时得到线段PO. 证明:由折叠知
折纸方案:如图,折叠三角形纸片BMN,使点N落在BM上,并使折痕经过点M,得到折痕MP,同时得到线段PO. 证明:由折叠知![]() ,
,
∴![]()
![]()
∴![]()
∵![]() ,∴
,∴![]()
∴![]() .∴
.∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了
 、
、 、
、 、
、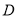 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.根据以上信息,解答下列问题:
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从
 、
、 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是 等级的概率.
等级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:


(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截下列图形,截面不能得到圆的立体图形是( )
A. 球B. 正方体C. 圆柱D. 圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】n边形的每个外角都为24°,则边数n为________ .
-
科目: 来源: 题型:
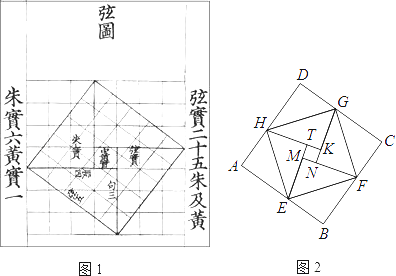
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=10,则S2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
相关试题

