【题目】关于x的一元二次方程x2﹣(m﹣3)x﹣m2=0.
(1)证明:方程总有两个不相等的实数根;
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|﹣2,求m的值及方程的根.
参考答案:
【答案】(1)证明见解析;(2)x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]() 或
或
【解析】试题分析:(1)根据一元二次方程的判别式△=b2﹣4ac的结果判断即可,当△>0时,有两个不相等的实数根,当△=0时,有两个相等的实数根,当△<0时,方程没有实数根;
(2)根据一元二次方程根与系数的关系x1+x2=-![]() ,x1x2=
,x1x2=![]() ,表示出两根的关系,得到x1,x2异号,然后根据绝对值的性质和两根的关系分类讨论即可求解.
,表示出两根的关系,得到x1,x2异号,然后根据绝对值的性质和两根的关系分类讨论即可求解.
试题解析:(1)一元二次方程x2﹣(m﹣3)x﹣m2=0,
∵a=1,b=﹣(m﹣3)=3﹣m,c=﹣m2,
∴△=b2﹣4ac=(3﹣m)2﹣4×1×(﹣m2)=5m2﹣6m+9=5(m﹣![]() )2+
)2+![]() ,
,
∴△>0,
则方程有两个不相等的实数根;
(2)∵x1x2=![]() =﹣m2≤0,x1+x2=m﹣3,
=﹣m2≤0,x1+x2=m﹣3,
∴x1,x2异号,
又|x1|=|x2|﹣2,即|x1|﹣|x2|=﹣2,
若x1>0,x2<0,上式化简得:x1+x2=﹣2,
∴m﹣3=﹣2,即m=1,
方程化为x2+2x﹣1=0,
解得:x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]() ,
,
若x1<0,x2>0,上式化简得:﹣(x1+x2)=﹣2,
∴x1+x2=m﹣3=2,即m=5,
方程化为x2﹣2x﹣25=0,
解得:x1=1﹣![]() ,x2=1+
,x2=1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然事件的是( )
A.掷一枚硬币,正面朝上B.某运动员跳高的最好成绩是20.1米
C.太阳从东方升起D.从车间刚生产的产品中任意抽取一件是次品
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,-3)到y轴的距离是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古代的房屋建筑中,窗棂是重要的组成部分,具有高度的艺术价值.下列窗棂的图案中,是中心对称图形但不是轴对称图形的是( )
A.
B.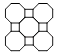
C.
D.
相关试题

