【题目】已知:有理数a、b、c在数轴上的位置如图所示,且|c|>|a|.
![]()
(1)若|a+10|=20,b2=400,c的相反数是30,求a、b、c的值;
(2)在(1)的条件下,a、b、c分别是A、B、C点在数轴上所对应的数,
①线段AC的长是________,将数轴折叠使得点A和点C重合,则折痕处在数轴上表示的数是__________
②数轴上是否存在一点P,使得P点到C点的距离加上P点到A点的距离减去P点到B点的距离为50,即PC+PAPB=50?若存在,求出P点在数轴上所对应的数;若不存在,请说明理由;
③点C,B分别以4个单位/秒和3个单位/秒的速度同时向右运动,点A以7个单位/秒的速度向右运动,是否存在常数m,使得3CA+2mOB-mOA为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
参考答案:
【答案】(1)a=10,b=20,c=-30;(2) ①40,-10;②存在;-90或![]() ;(2)存在m=9,定值是390.
;(2)存在m=9,定值是390.
【解析】
(1)利用绝对值的性质和数轴即可求出a,利用b2=400和数轴即可求出b,利用c的相反数即可求出c;
(2)①利用数轴上两点之间的距离公式即可求出AC,再利用中点公式即可求出折痕所表示的数;
②设P表示的数为![]() ,根据P点不同的位置及数轴上两点的距离公式分类讨论即可;
,根据P点不同的位置及数轴上两点的距离公式分类讨论即可;
③设运动时间为t,利用数轴上两点之间的距离公式,表示出CA、OB、OA,将它们代入3CA+2mOB-mOA并化简,再根据其为定值,即与t值无关,令t的系数为0即可.
解:(1)∵|a+10|=20,b2=400,c的相反数是30
解得a=﹣30或10,b=±20,c=﹣30
由数轴可知:a>0,b>0
∴a=10,b=20,c=﹣30
(2)①根据数轴上两点之间的距离公式:AC=| a-c|=40;
若A、C两点重合,则折痕在数轴上所表示的点即为AC的中点,故折痕处在数轴上表示的数是![]() ;
;
②存在,求法如下
假设P点所表示的数为![]() ,
,
当P在C左侧时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=﹣30-![]() ,PA=10-
,PA=10-![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50,
∴(﹣30-![]() )+(10-
)+(10-![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() .
.
若P在C、A之间时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=10-
,PA=10-![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50
(![]() )+(10-
)+(10-![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() ,不符合前提,故舍去;
,不符合前提,故舍去;
若P在A、B之间时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=
,PA=![]() ,PB=20-
,PB=20-![]()
根据PC+PAPB=50
(![]() )+(
)+(![]() )-(20-
)-(20-![]() )=50
)=50
解得:![]() ;
;
若P在B右侧时,即![]() ,如下图所示:
,如下图所示:
![]()
∴PC=![]() ,PA=
,PA=![]() ,PB=
,PB=![]()
根据PC+PAPB=50
(![]() )+(
)+(![]() )-(
)-(![]() )=50
)=50
解得:![]() ,不符合前提,故舍去;
,不符合前提,故舍去;
综上所述:P点在数轴上所对应的数是:-90或![]() .
.
③存在,理由如下:
设运动时间为t,此时C表示的数为:﹣30+4t,A表示的数为:10+7t,B表示的数为20+3t.
![]()
∴AC=(10+7t)-(﹣30+4t)=3t+40,OA=10+7t,OB=20+3t代入3CA+2mOB-mOA中得:
原式=3(3t+40)+2m(20+3t)-m(10+7t)
=(9-m)t+120+30m
∵3CA+2mOB-mOA为定值,即与t值无关,令t 的系数为0即可,
∴9-m=0,解得:
m=9,代入得:
定值=120+30×9=390.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,根据图像信息,以上说法正确的是( )
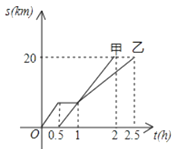
A.甲和乙两人同时到达目的地;B.甲在途中停留了0.5h;
C.相遇后,甲的速度小于乙的速度;D.他们都骑了20km
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把8块相同的小长方形地砖拼成一块大长方形地砖.

(1)每块小长方形地砖的长和宽分别是多少?(要求列方程组进行解答)
(2)小明想用一块面积为
 的正方形地毯,沿着边的方向裁剪出一块新的长方形地毯,用来盖住这块大长方形地砖你帮小明算一算,他能剪出符合要求的地毯吗?
的正方形地毯,沿着边的方向裁剪出一块新的长方形地毯,用来盖住这块大长方形地砖你帮小明算一算,他能剪出符合要求的地毯吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在春节期间搞优惠促销活动,商场将29英寸和25英寸彩电共96台分别以8折和7折出售,共得168400元。已知29英寸彩电原价为3000元/台,25英寸彩电原价为2000元/台,出售29英寸和25英寸彩电各多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:①AP=EF,②△APD一定是等腰三角形,③∠PFE=∠BAP,④PD=
 EC.其中正确结论的序号是( )
EC.其中正确结论的序号是( )
A.①②④B.②④C.①②③D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2
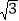 cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )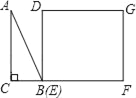
A.
 B.
B. 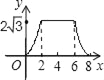 C.
C. 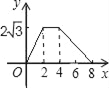 D.
D. 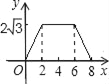
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
相关试题

