【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A型电器销售单价为200元,B型电器销售单价150元;(2)最多能采购37台;(3)方案一:采购A型36台B型14台;方案二:采购A型37台B型13台.
【解析】
(1)设A、B两种型号电器的销售单价分别为x元、y元,根据3台A型号4台B型号的电器收入1200元,5台A型号6台B型号的电器收入1900元,列方程组求解;
(2)设采购A种型号电器a台,则采购B种型号电器(50a)台,根据金额不多余7500元,列不等式求解;
(3)根据A型号的电器的进价和售价,B型号的电器的进价和售价,再根据一件的利润乘以总的件数等于总利润列出不等式,再进行求解即可得出答案.
解:(1)设A型电器销售单价为x元,B型电器销售单价y元,
则![]() ,
,
解得:![]() ,
,
答:A型电器销售单价为200元,B型电器销售单价150元;
(2)设A型电器采购a台,
则160a+120(50a)≤7500,
解得:a≤![]() ,
,
则最多能采购37台;
(3)设A型电器采购a台,
依题意,得:(200160)a+(150120)(50a)>1850,
解得:a>35,
则35<a≤![]() ,
,
∵a是正整数,
∴a=36或37,
方案一:采购A型36台B型14台;
方案二:采购A型37台B型13台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长为
 的大正方形中剪去一个边长为
的大正方形中剪去一个边长为 的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,下列四种割拼方法中,能够验证平方差公式的有( )
的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,下列四种割拼方法中,能够验证平方差公式的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如图.

请根据图中信息,解答下列问题
(1)该调查抽取的学生数量为_________,
 ________
________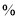 ,“常常”对应扇形的圆心角为_______;
,“常常”对应扇形的圆心角为_______;(2)请你补全条形统计图;
(3)若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )

A. EF=2CE B. S△AEF=
 S△BCF C. BF=3CD D. BC=
S△BCF C. BF=3CD D. BC= AE
AE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于
 AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
AB的长为半径画弧,两弧相交于点M、N;②作直线MN交AC于点D,连接BD.若CD=CB,∠A=35°,则∠C等于( )
A. 40° B. 50° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】联合国规定每年6月25日是“世界环境日”,某校编写了关于环境保护的
 个问答题让学生学习,为了解学生对
个问答题让学生学习,为了解学生对 个问答题的掌握情况,随机抽查了部分学生进行答题测试,并根据测试结果得出下面两个不完整的统计图,请根据统计图提供的信息,回答下列问题(其中
个问答题的掌握情况,随机抽查了部分学生进行答题测试,并根据测试结果得出下面两个不完整的统计图,请根据统计图提供的信息,回答下列问题(其中 分别表示答对
分别表示答对 个题,答对
个题,答对 个题,答对
个题,答对 个题,答对
个题,答对 个题,答对
个题,答对 个题的人数) :
个题的人数) :
(1)参加测试的学生有多少人?其中“答对个
 题”的有多少人数?
题”的有多少人数?(2)把条形统计图补充完整;
(3)若该校共有
 名学生,估计该校能“答对
名学生,估计该校能“答对 个题”以上(含
个题”以上(含 个题)的人数
个题)的人数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象经过点A(1,3).
的图象经过点A(1,3).(1)试确定此反比例函数的解析式;
(2)当
 =2时, 求y的值;
=2时, 求y的值;(3)当自变量
 从5增大到8时,函数值y是怎样变化的?
从5增大到8时,函数值y是怎样变化的?
相关试题

