【题目】老师在黑板上写了一个等式:(a+3)x=4(a+3).王聪说x=4,刘敏说不一定,当x≠4时,这个等式也可能成立.你同意谁的观点?请用等式的基本性质说明理由.
参考答案:
【答案】同意刘敏的观点,理由详见解析.
【解析】
分当a+3=0时,当a+3≠0时两种情况解答即可.
解:同意刘敏的观点,理由如下:
当a+3=0时,x为任意实数;
当a+3≠0时,等式两边同时除以(a+3),得x=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,请根据这组数的规律写出第10个数是( )
A.25
B.27
C.55
D.120 -
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的基本性质填空,并说明运用了等式的哪条基本性质.
(1)如果3x+7=8,那么3x=8-________;
(2)如果2x=5-3x,那么2x+________=5;
(3)如果2x=10,那么x=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°,求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
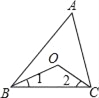
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不论x取何值,等式2ax+b=4x-3总成立,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?
相关试题

