【题目】如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)若AC⊥BC,且AC=8,BC=6,求切线GE的长.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)连接OE、OG,由已知易证OG是△ACD的中位线,由此可得OG∥AC,结合OE=OC,由平行线的性质和等腰三角形的性质可证得∠EOG=∠DOG,从而可证得△EOG≌△DOG,由此可得∠OEG=∠ODG=90°,即可证得EG是⊙O的切线;
(2)由已知条件易得AB=10,GD是⊙O的切线,则GE=GD,在Rt△ACD和Rt△BCD中,由AC2-AD2=CD2,BC2-BD2=CD2可得AC2-AD2=BC2-BD2,设BD=x,则AD=10-x,列出方程解得x的值,即可得到AD的长,从而得到GD的长就可得到GE的长了.
试题解析:
(1)连接OE,OG;
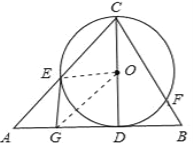
∵AG=GD,CO=OD,
∴OG是△ACD的中位线,
∴OG∥AC.
∴∠OEC=∠GOE,∠ACD=∠GOD.
∵OE=OC,
∴∠ACD=∠OEC.
∴∠GOD=∠GOE.
∵OE=OD,OG=OG,
∴△OEG≌△ODG.
∴∠OEG=∠ODG=90°.
∴GE是⊙O的切线.
(2)∵AC=8,BC=6,
∴AB=![]() =10.
=10.
∴OD⊥GD.
∴GD也是圆O的切线.
∴GD=GE.
设BD=x,则AD=10﹣x,
在Rt△CDA和Rt△CDB中,
由勾股定理得:CD2=82﹣(10﹣x)2,CD2=62﹣x2
∴82﹣(10﹣x)2=62﹣x2
解得x=![]() ,
,
∴AD=10﹣![]() =
=![]() .
.
又∵点G是AD的中点,
∴GE=GD=![]() AD=
AD=![]() .
.
即切线GE的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,每个小正方形的边长为
 点
点 均为格点(格点是指每个小正方形的顶点).
均为格点(格点是指每个小正方形的顶点).
 标出格点
标出格点 使线段
使线段 ;
; 标出格点
标出格点 ,使
,使 是
是 中
中 边上的高;
边上的高; 到
到 的距离为 ;
的距离为 ; 求
求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行
 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的 倍,结果比其他班提前
倍,结果比其他班提前 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+x的图象,如图所示.
(1)在同一直角坐标系中用描点法画出一次函数y=
 x+
x+ 的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值;
的图象,观察图象写出自变量x取值在什么范围时,一次函数的值小于二次函数的值;(2)如图,点P是坐标平面上的一点,并在网格的格点上,请选择一种适当的平移方法,使平移后二次函数图象的顶点落在P点上,写出平移后二次函数图象的函数表达式,并判断点P是否在函数y=
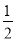 x+
x+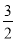 的图象上,请说明理由.
的图象上,请说明理由.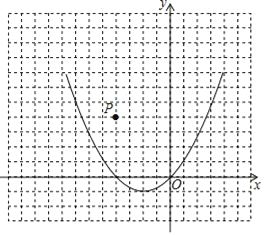
-
科目: 来源: 题型:
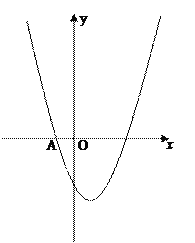
查看答案和解析>>【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
① 当点P' 落在该抛物线上时,求m的值;
② 当点P' 落在第二象限内,P'A2取得最小值时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
 B.
B.  C.
C.  D.
D. 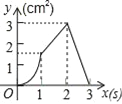
相关试题

