【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。
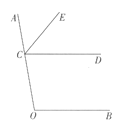
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF=![]() ∠COB。
∠COB。
(理由: _____________________________________)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
参考答案:
【答案】(1)补图见解析;(2)证明见解析.
【解析】试题分析:(1)本题根据已知条件画出图形即可. (2)本题根据角平分线的定义和等量代换即可求出.
试题解析:(1)
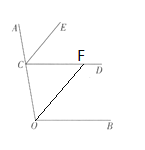
(2)∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=_![]() ∠ACD ,∠COF=
∠ACD ,∠COF=![]() ∠COB。
∠COB。
(理由: 角平分线的性质)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠ COB 。
(理由: 等量代换)
∴∠ACE=∠COF。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年“中国好声音”全国巡演重庆站在奥体中心举行.童童从家出发前往观看,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出结束后,童童搭乘邻居刘叔叔的车顺利到家.其中x表示童童从家出发后所用时间,y表示童童离家的距离.下图能反映y与x的函数关系式的大致图象是( )
A.
 B.
B.  C.
C. 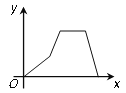 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国家政策的宏观调控下,某市的商品房成交价由今年3月份的14000元/m2下降到5月份的12600元/m2
(1)问4、5两月平均每月降价的百分率是多少?(参考数据:
 ≈0.95)
≈0.95)(2)如果房价继续回落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌破10000元/m2?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一下数据75,80,80,85,90中,众数、中位数分别是( )
A、75,80 B、80,80 C、80,85 D、80,90
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店出售某种商品每件可获利m元,利润率为20%,若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m元,则提价后的利润率为( )
A. 25% B. 20% C. 16% D. 12.5%
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内定义一种运算“﹡”,其规则为a﹡b=a2﹣b2 , 根据这个规则,求方程(x﹣2)﹡1=0的解为 .
相关试题

