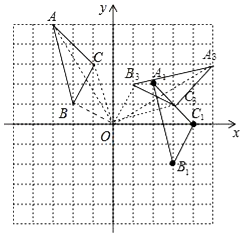
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标,并画出△A3B3C3 .
参考答案:
【答案】
(1)
解:如图,△A1B1C1为所作.
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)
解:因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)
解:如图,△A2B3C3为所作,
A3(5,3),B3(1,2),C3(3,1).

【解析】(1)分别确定三个顶点平移后的对应点,顺次连接可得;(2)根据中心对称的性质可得;(3)分别作出三个顶点绕着点O按顺时针方向旋转90°得到的对应点,顺次连接可得.
【考点精析】根据题目的已知条件,利用平移的性质和中心对称及中心对称图形的相关知识可以得到问题的答案,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣24﹣
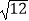 +|1﹣2
+|1﹣2 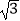 |+(
|+( 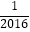 )﹣1+(π﹣
)﹣1+(π﹣  )0 .
)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和等于1800°,则这个多边形是_____边形;如果一个n边形每一个内角都是135°,则n=_____;如果一个n边形每一个外角都是36°,则n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
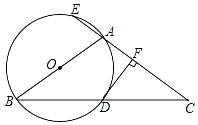
(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求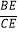 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

相关试题

