搜索
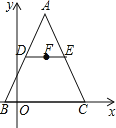
【题目】如图，在△ABC中，AB=AC=13，DE是△ABC的中位线，F是DE的中点，已知B（-1,0），C（9,0），则点F的坐标为______________.
参考答案：
【答案】（4,6）
【解析】如图，延长AF交BC于点G．易证DF是△ABG的中位线，由三角形中位线定理可以求得点F的坐标．
解：如图，延长AF交BC于点G．
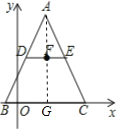
∵B（-1，0），C（9，0），
∴BC=10．
∵AB=AC=13，DE是△ABC的中位线，F是DE的中点，
∴AG⊥BC，则BG=CG=5．
∴G（4，0）
∴在直角△ABG中，由勾股定理得
AG=
=12．
则F（4，6）．
故答案是：（4，6）．
“点睛”本题考查了三角形中位线定理和坐标与图形性质．利用勾股定理求得AG的长度是解题的关键．
-
科目： 来源： 题型：
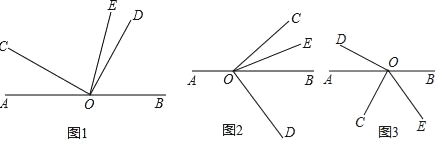
查看答案和解析>>【题目】已知直线AB经过点O，∠COD=90°，OE是∠BOC的平分线．
（1）如图1，若∠AOC=50°，求∠DOE；
（2）如图1，若∠AOC=α，求∠DOE；（用含α的式子表示）
（3）将图1中的∠COD绕顶点O顺时针旋转到图2的位置，其它条件不变，（2）中的结论是否还成立？试说明理由；
（4）将图1中的∠COD绕顶点O逆时针旋转到图3的位置，其它条件不变，求∠DOE.（用含α的式子表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD中，∠D=135°，AD=6，CE=2
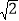，点P是线段AC上一动点，点F是线段AB上一动点，则PE+PF的最小值是（ ）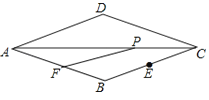
A. 3 B. 6 C. 2
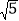D. 3 -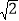
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形ABCO放在直角坐标系中，其中顶点B的坐标为(10， 8)，E是BC边上一点将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y=
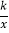的图象与边AB交于点F, 则线段AF的长为( ) 
A.
B. 2 C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC为等边三角形，AB=2，点D为边AB上一点，过点D作DE∥AC，交BC于E点；过E点作EF⊥DE，交AB的延长线于F点．设AD=x，△DEF的面积为y，则能大致反映y与x函数关系的图象是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题8分）△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．
（1）按要求作图：
①画出△ABC关于原点O的中心对称图形△A1B1C1；
②画出将△ABC绕点A逆时针旋转90°得到△AB2C2，
（2）回答下列问题：
①△A1B1C1中顶点A1坐标为 ；②若P（a，b）为△ABC边上一点，则按照（1）中①作图，点P对应的点P1的坐标为 ．
【答案】（1）作图见解析；（2）（1，-2）（-a,-b）
【解析】试题分析：（1）首先找出对应点的位置，再顺次连接即可；
（2）①根据图形可直接写出坐标；②根据关于原点对称点的坐标特点可得答案．
试题解析：（1）如图所示：
（2）①根据图形可得A1坐标为（2，﹣4）；
②点P1的坐标为（﹣a，﹣b）．
故答案为：（﹣2，﹣4）；（﹣a，﹣b）．
考点：作图-旋转变换．
【题型】填空题
【结束】
23【题目】在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：
（1）本次抽查活动中共抽查了 名学生；
（2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．
①试估算：该校九年级视力不低于4.8的学生约有 名；
②请你帮忙估算出该校视力低于4.8的学生数．
-
科目： 来源： 题型：
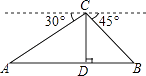
查看答案和解析>>【题目】4月26日，2015黄河口（东营）国际马拉松比赛拉开帷幕，中央电视台体育频道用直升机航拍技术全程直播．如图，在直升机的镜头下，观测马拉松景观大道A处的俯角为30°，B处的俯角为45°．如果此时直升机镜头C处的高度CD为200米，点A、D、B在同一直线上，则AB两点的距离是米．
相关试题
