【题目】若n是正整数,且x2n=5,则(2x3n)2÷(4x2n)= .
参考答案:
【答案】25
【解析】解:∵n是正整数,且x2n=5,
∴(2x3n)2÷(4x2n)
=4x6n÷(4x2n)
=(4÷4)x6n﹣2n
=x4n
=(x2n)2
=52
=25.
所以答案是:25.
【考点精析】解答此题的关键在于理解代数式求值的相关知识,掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入,以及对单项式除以单项式的理解,了解单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同他的指数一起作为商的一个因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB上有两点C,D,且AC∶CD∶DB=2∶3∶4,E,F分别为AC,DB的中点,EF=2.4 cm,求线段AB的长.
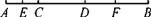
-
科目: 来源: 题型:
查看答案和解析>>【题目】690000用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将某图形的横坐标都减去2,纵坐标不变,则该图形( )
A.向右平移2个单位
B.向左平移2个单位
C.向上平移2个单位
D.向下平移2个单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,∠A=50°,则∠B=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
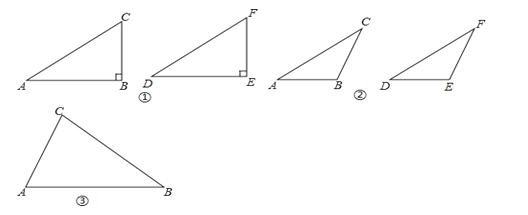
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据______,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若______,则△ABC≌△DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

相关试题

