【题目】下列说法正确的是( )
A. 哥哥的身高比弟弟高是必然事件
B. 今年的12月1日有雨是不确定事件
C. 随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D. “彩票中奖的概率为![]() ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
参考答案:
【答案】B
【解析】A选项,因为现实生活中,哥哥的身高比弟弟矮的也不少,所以A选项的说法是错误的;
B选项,因为今年12月1日有没有雨是一个随机事件,所以B选项的说法正确;
C选项,因为随机掷一枚硬币,正面向上是个随机事件,连续抛掷一枚硬币两次正面都向上也是一个随机事件,所以C说法错误;
D选项,“彩票的中奖概率为![]() ”说的是“每买一张彩票,有
”说的是“每买一张彩票,有![]() 的机会中奖”,即“你买第一张中奖机会是
的机会中奖”,即“你买第一张中奖机会是![]() ,买第二张的时候中奖机会还是
,买第二张的时候中奖机会还是![]() ,而不是累计到中奖机会为
,而不是累计到中奖机会为![]() ”,所以D选项的说法是错误的;
”,所以D选项的说法是错误的;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是

A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
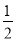 m2-n(mn2)2;
m2-n(mn2)2;(2)(x2-2x)(2x+3)÷(2x);
(3)(2x+y)(2x-y)+(x+y)2-2(2x2+xy);
(4)(ab-b2)÷
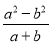 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形每一个内角都等于120°,则从此多边形一个顶点出发可引的对角线的条数是( )
A.5条B.4条C.3条D.2条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a﹣3|=3﹣a,下列成立的是( )
A.a>3B.a<3C.a≥3D.a≤3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由

∵∠1=∠2 ( )
∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴_______∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )
相关试题

