【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

参考答案:
【答案】(1)当 h=50 时,t1=![]() (秒);当 h=100 时,t2=2
(秒);当 h=100 时,t2=2![]() (秒);(2)t2 是 t1 的
(秒);(2)t2 是 t1 的![]() 倍;(3)下落的高度是 11.25 米.
倍;(3)下落的高度是 11.25 米.
【解析】
(1)将h=50代入t1=![]() 进行计算即可;将h=100代入t2=
进行计算即可;将h=100代入t2=![]() 进行计算即可;
进行计算即可;
(2)计算t2与t1的比值即可得出结论;
(3)将t=1.5代入公式t=![]() 进行计算即可.
进行计算即可.
(1)当 h=50 时,t1=![]() =
=![]() (秒);
(秒);
当 h=100 时,t2=![]() =
=![]() =2
=2![]() (秒);
(秒);
(2)∵![]() =
=![]() ,
,
∴t2 是 t1 的![]() 倍.
倍.
(3)当 t=1.5 时,1.5=![]() , 解得 h=11.25,
, 解得 h=11.25,
∴下落的高度是 11.25 米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的条形统计图与扇形统计图:依据图中信息,得出下列结论:

(1)接受这次调查的家长人数为200人;
(2)在扇形统计图中,“不赞同”的家长部分所对应的扇形圆心角大小为162°;
(3)表示“无所谓”的家长人数为40人;
(4)随机抽查一名接受调查的家长,恰好抽到“很赞同”的家长的概率是 .
.
其中正确的结论个数为( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,OD⊥OE.
(1)请你数一数,图中有多少个角?(备注:小于平角的角);
(2)请通过计算说明OE是否平分∠BOC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,
, .点
.点 的坐标为(
的坐标为(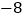 ,0),点
,0),点 的坐标为(
的坐标为( ,0).
,0).(1)求
 的值;
的值;(2)若点
 (
( ,
, )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点 运动过程中,试写出
运动过程中,试写出 的面积
的面积 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)探究:当
 运动到什么位置时,
运动到什么位置时, 的面积为
的面积为 ,并说明理由.
,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
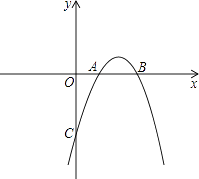
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第
 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;(5)如果第
 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表:
甲
乙
进价(元/部)
4000
2500
售价(元/部)
4300
3000
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
相关试题

