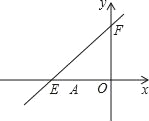
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
试题(1)将点E坐标(-8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(-6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为![]() 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,
∴k=![]() ;
;
(2)∵k=![]() ,
,
∴直线的解析式为:y=![]() x+6,
x+6,
∵P点在y=![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),
x+6),
∴△OPA以OA为底的边上的高是|![]() x+6|,
x+6|,
当点P在第二象限时,|![]() x+6|=
x+6|=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6.
∴S=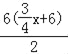 =
=![]() x+18.
x+18.
∵P点在第二象限,
∴﹣8<x<0;
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,
,
解得|n|=![]() ,
,
则n1=![]() 或者n2=﹣
或者n2=﹣![]() (舍去),
(舍去),
当n=![]() 时,
时,![]() =
=![]() m+6,
m+6,
则m=﹣![]() ,
,
故P(﹣![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,把两数相乘,积为1的是( )
A.2和-2
B.-2和
C. 和
和 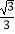
D. 和-
和- 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3,
 ),B(9,5
),B(9,5  ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,  ,
,  (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.
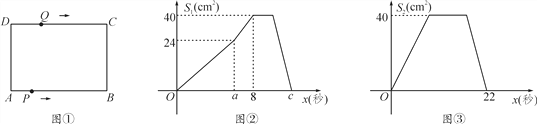
(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
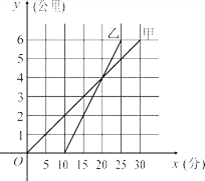
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读,我们知道,在数轴上,x=1表示一个点,而在平面坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形,就是一次函数y=2x+1的图象,它也是一条直线,如图1,可以得出,直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组
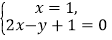 的解,所以这个方程组的解为
的解,所以这个方程组的解为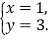
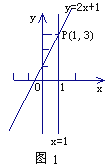
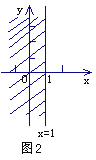
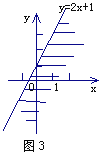
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧的部分,如图2;y≤2x+1,也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3.
回答下列问题:
(1)在直角坐标系(如图4)中,用作图的方法求方程组
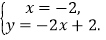 的解;
的解;(2)用阴影表示
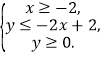 所围成的区域.
所围成的区域. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长.
相关试题

