【题目】阅读下列材料: 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式; 当4<x≤16时,写出一个符合表中数据的函数解析式;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min. 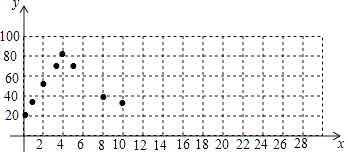
参考答案:
【答案】
(1)50
(2)y=15x+20;y= ![]()
(3)56
【解析】解:(1.)由题意可知2分钟温度上升30°C,所以m=50,所以答案是50. (2.)①当0≤x≤4时,函数解析式是一次函数,y=15x+20.
②当4<x≤16时,函数解析式是反比例函数y= ![]() .所以答案是y=15x+20,y=
.所以答案是y=15x+20,y= ![]() .
.
(3.)函数图象如图所示,
(4.)观察图象可知预测水温第8次达到40℃时,距离接通电源8min.
所以答案是8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点
 按如图方式叠放在一起,当
按如图方式叠放在一起,当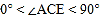 且点
且点 在直线
在直线 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示: ,
, ,
, .
.
(1)①若
 ,则
,则 的度数为 ;
的度数为 ;②若
 ,则
,则 的度数为 ;
的度数为 ;(2)由(1)猜想
 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出
 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

-
科目: 来源: 题型:
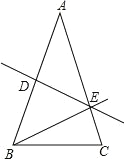
查看答案和解析>>【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


-
科目: 来源: 题型:
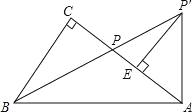
查看答案和解析>>【题目】如图,在 Rt△ABC 中,∠C=90°,AP′⊥AB,BP′交 AC 于点 P, AP=AP′.
(1)求证:∠CBP=∠ABP;
(2)过点 P′作 P′E⊥AC 于点 E,求证:AE=CP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在△DBC 中,DB=DC,A 为△DBC 外一点,且∠BAC=∠BDC,DM⊥AC 于 M.
(1)求证:AD 平分△ABC 的外角;
(2)判断 AM、AC、AB 有怎样的数量关系,并证明你的结论.

相关试题

