【题目】(阅读理解)若数轴上两点![]() ,
,![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,则有:
,则有:
①![]() ,
,![]() 两点的中点表示的数为
两点的中点表示的数为![]() ;
;
②![]() ,
,![]() 两点之间的距离
两点之间的距离![]() ;若
;若![]() ,则可简化为
,则可简化为![]() .
.
(解决问题)数轴上两点![]() ,
,![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() .
.
(1)求出![]() ,
,![]() 两点的中点
两点的中点![]() 表示的数;
表示的数;
(2)点![]() 从原点
从原点![]() 点出发向右运动,经过
点出发向右运动,经过![]() 秒后点
秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的
点距离的![]() 倍,求点
倍,求点![]() 的运动速度是每秒多少个单位长度?
的运动速度是每秒多少个单位长度?
(数学思考)
(3)点![]() 以每秒
以每秒![]() 个单位的速度从原点
个单位的速度从原点![]() 出发向右运动,同时,点
出发向右运动,同时,点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位的速度向左运动,点
个单位的速度向左运动,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度向右运动,
个单位的速度向右运动,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.思考:在运动过程中,
的中点.思考:在运动过程中,![]() 的值是否发生变化?如果没有变化,请求出这个值;如果发生变化,请说明理由.
的值是否发生变化?如果没有变化,请求出这个值;如果发生变化,请说明理由.
参考答案:
【答案】(1)3;(2)点D的运动速度是每秒![]() 个单位长度,或每秒4个单位长度;(3)不变,
个单位长度,或每秒4个单位长度;(3)不变,![]()
【解析】
(1)根据非负数的性质和中点坐标的求法即可得到结论;
(2)设点D的运动速度为v,①当点D运动到点C左边时,②当点D运动到点C右边时,根据题意列方程即可得到结论;
(3)设运动时间为t,则点E对应的数是t,点M对应的数是27t,点N对应的数是8+10t.根据题意求得P点对应的数是![]() =13t,Q点对应的数是
=13t,Q点对应的数是![]() =4+5t,于是求得结论.
=4+5t,于是求得结论.
解:(1)∵|a+2|+(b-8)2020=0
∴a=-2,b=8,
∴A、B两点的中点C表示的数是:![]() =3;
=3;
(2)设点D的运动速度为v,
①当点D运动到点C左边时:由题意,有2v-(-2)=2(3-2v),
解之得v=![]()
②当点D运动到点C右边时:由题意,有2v-(-2)=2(2v-3),
解之得v=4;
∴点D的运动速度是每秒![]() 个单位长度,或每秒4个单位长度;
个单位长度,或每秒4个单位长度;
(3)设运动时间为t,则点E对应的数是t,点M对应的数是-2-7t,点N对应的数是8+10t.
∵P是ME的中点,
∴P点对应的数是![]() =13t,
=13t,
又∵Q是ON的中点,
∴Q点对应的数是![]() =4+5t,
=4+5t,
∴MN=(8+10t)-(-2-7t)=10+17t,OE=t
PQ=(4+5t)-(-1-3t)=5+8t,
∴![]()
∴![]() 的值不变,等于2.
的值不变,等于2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对某一个函数给出如下定义:若存在实数
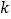 ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点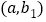 ,
,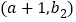 ,
,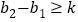 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的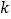 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数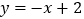 ,当
,当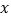 取值
取值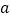 和
和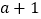 时,函数值分别为
时,函数值分别为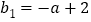 ,
,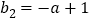 ,故
,故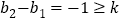 ,因此函数
,因此函数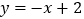 是限减函数,它的限减系数为
是限减函数,它的限减系数为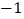 .
.(1)写出函数
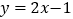 的限减系数;
的限减系数;(2)
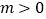 ,已知
,已知 (
(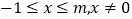 )是限减函数,且限减系数
)是限减函数,且限减系数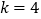 ,求
,求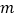 的取值范围.
的取值范围.(3)已知函数
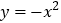 的图象上一点
的图象上一点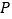 ,过点
,过点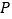 作直线
作直线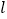 垂直于
垂直于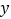 轴,将函数
轴,将函数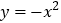 的图象在点
的图象在点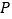 右侧的部分关于直线
右侧的部分关于直线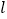 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数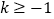 ,直接写出
,直接写出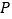 点横坐标
点横坐标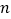 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1),B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,则一次变换后顶点C的坐标为____,如果这样连续经过2 017次变换后,等边△ABC的顶点C的坐标为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表中给出的是某月的月历,任意选取“
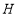 ”型框中的
”型框中的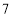 个数(如阴影部分所示).请你运用所学的数学知识来研究,则这
个数(如阴影部分所示).请你运用所学的数学知识来研究,则这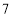 个数的和不可能是( )
个数的和不可能是( )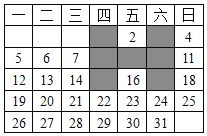
A.
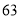 B.
B.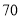 C.
C.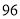 D.
D.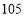
-
科目: 来源: 题型:
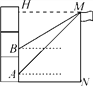
查看答案和解析>>【题目】如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1 m.
(1)AB=________m;
(2)求旗杆MN的高度.(结果保留两位小数)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
-
科目: 来源: 题型:
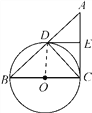
查看答案和解析>>【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
(1)求证:DE是⊙O的切线;
(2)若BD=4,CD=3,求AC的长.
相关试题

