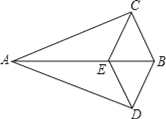
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证△BED≌△CFD.
(2)已知EC=6,AC=10,求BE.
(3)当∠C=45°时,判断△DFC的周长与线段AC长度的关系,并说明理由.

参考答案:
【答案】(1)见解析;(2)2;(3)△DFC的周长等于AC的长度,理由见解析.
【解析】
(1)由已知条件根据“HL”即可证得△BED≌△CFD;
(2)由已知易得AE=8,由(1)中所得△BED≌△CFD可得DE=DF,结合AD=AD,∠AED=∠AFD=90°可得△AED≌△AFD,由此可得AE=AF=AC-CF,再结合BE=CF即可得到AE=AC-BE,从而可得BE=AC-AE=10-8=2;
(3)当∠C=45°时,易得△AEC是等腰直角三角形,结合(2)中所得AE=AF可得CE=AE=AF,结合DF=DE即可得到△DCF的周长=DC+DF+FC=DC+DE+FC=CE+FC=AF+FC=AC.
(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
∵在Rt△BED和Rt△CFD中,BE=CF,BD=CD,
∴Rt△BED≌ Rt△CFD(HL);
(2)∵DE⊥AE,EC=6,AC=10,
∴在Rt△AEC中,AE=![]() ,
,
由(1)中所得Rt△BED≌ Rt△CFD可得DE=DF,
∵在△AED和△AFD中,DE=DF,AD=AD,∠E=∠AFD=90°,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF ,
又∵AF=AC-CF,
∴AE=AC-CF ,
又∵BE=CF ,
∴AE=AC-B E ,即8=10-BE ,
∴BE=2 ;
(3)△DFC的周长等于AC的长度,理由如下:
∵∠C=45°,∠E=90°,
∴△AEC为等腰直角三角形,
∴AE=EC,
∵由(2)可知AE=AF,
∴AF=EC,
又∵DE=DF,
∴△DFC的周长=CD+DF+FC=CD+DE+FC=CE+FC=AF+FC=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣
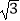 x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣  (x﹣
(x﹣ 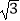 )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
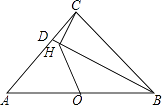
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元.购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)实验中学实际需要一次性购买足球和篮球共96个.要求购买足球和篮球的总费用不超过5800元,这所中学最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
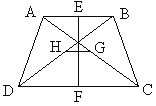
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
相关试题

