【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
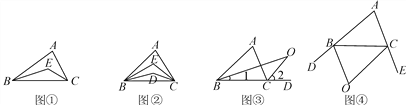
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
参考答案:
【答案】问题:130°,90°+![]() n°探究:(1)60°+
n°探究:(1)60°+![]() n°(2)∠BOC=
n°(2)∠BOC=![]() ∠A. (3)∠BOC=90°-
∠A. (3)∠BOC=90°-![]() ∠A
∠A
【解析】试题分析:问题:利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用角平分线的定义求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;将∠A的度数换成n°,然后求解即可;
探究:(1)利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用三等分角求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,再根据角平分线的定义可得∠ABC=2∠OBC,∠ACD=2∠OCD,然后整理即可得解;
(3)根据平角的定义以及角平分线的定义表示出∠OBC和∠OCB,然后根据三角形的内角和定理列式表示出∠BOC,然后整理即可得解.
试题解析:【问题】解:∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°,
×100°=50°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-50°=130°;
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=90°-
×(180°-n°)=90°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(90°-![]() n°)=90°+
n°)=90°+![]() n°;
n°;
探究:解:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=120°-
×(180°-n°)=120°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(120°-![]() n°)=60°+
n°)=60°+![]() n°;
n°;
(2)∠BOC=![]() ∠A.
∠A.
理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,
∠OCD=∠BOC+∠OBC,
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC),
∴∠A=2∠BOC,
∴∠BOC=![]() ∠A;
∠A;
(3)∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,
∴∠OBC=![]() (180°-∠ABC)=90°-
(180°-∠ABC)=90°-![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,
∠ACB,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-(90°-![]() ∠ABC)-(90°-
∠ABC)-(90°-![]() ∠ACB)=
∠ACB)=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A,
∴∠BOC=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a8÷a2=a6B. (a+b)2=a2+b2
C. a2a3=a6D. (﹣a2)3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x2+4xy﹣2x﹣3,B=﹣x2+xy+2,且3A+6B的值与x无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司产销一种产品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C是商品件数x的二次函数,调查数据如表:
产销商品件数(x/件)
10
20
30
产销成本(C/元)
120
180
260
商品的销售价格(单位:元)为P=35﹣
 x(每个周期的产销利润=Px﹣C)
x(每个周期的产销利润=Px﹣C)(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.
-
科目: 来源: 题型:
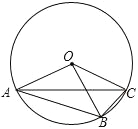
查看答案和解析>>【题目】如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,
(1)求证:∠ACB=2∠BAC;
(2)若AC平分∠OAB,求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )

A.点A的左边
B.点A与点B之间,靠近点A
C.点B与点C之间,靠近点B
D.点C的右边 -
科目: 来源: 题型:
查看答案和解析>>【题目】将2.017×10-4化为小数的是( )
A. 20170 B. 2017 C. 0.002017 D. 0.0002017
相关试题

