【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
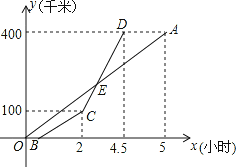
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
参考答案:
【答案】(1)y=120x-140(2≤x≤4.5);(2)E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;(3)![]() 、
、![]() 、
、![]() 、
、![]() .
.
【解析】
试题(1)设线段CD对应的函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)根据两图象相交的交点指的是两车相遇解答即可.
(3)先由货车和轿车相距30千米列出方程解答即可.
试题解析:(1)设线段CD对应的函数解析式为y=kx+b,
可得:![]() ,
,
解得:![]() .
.
所以线段CD对应的函数表达式为:y=120x-140(2≤x≤4.5);
(2)由图象可得:直线OA的解析式为:y=80x,
根据两图象相交的交点指的是两车相遇,
可得:80x=120x-140,
解得:x=3.5,
把x=3.5代入y=80x,得:y=280;
所以E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;
(3)设货车出发xh后,
可得:120x-140-30=80x,
解得:x=4.25.
故答案为:4.25.
(3)由题意知,B(![]() ,0),
,0),
∴BC段解析式为y=60x-20(![]() ≤x≤2),
≤x≤2),
货车与轿车相距30km有四种情况:
1)当![]() ≤x≤2时,80x-(60x-20)=30,解得x=
≤x≤2时,80x-(60x-20)=30,解得x=![]() ;
;
2)当2<x≤![]() 时,80x-(120x-140)=30,解得x=
时,80x-(120x-140)=30,解得x=![]() ;
;
3)当![]() <x≤
<x≤![]() 时,120x-140-80x=30,解得x=
时,120x-140-80x=30,解得x=![]() ;
;
4)当![]() <x≤5时,400-80x=30,解得x=
<x≤5时,400-80x=30,解得x=![]() ;
;
∴x=![]() 、
、![]() 、
、![]() 、
、![]() .
.
-
科目: 来源: 题型:
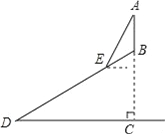
查看答案和解析>>【题目】如图,某班数学兴趣小组利用数学活动课时间测量位于山顶的电视塔AB的高度,已知山的坡度为30°,山高857.5尺,组员从山脚D处沿山坡向着电视塔方向前进1620尺到达E点,在点E处测得电视塔顶端A的仰角为60°,求电视塔AB的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2
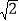 ,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
A. 2B.
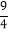 C.
C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
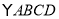 中
中 ,
,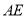 平分
平分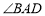 交
交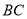 点
点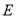 ,
,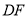 平分
平分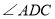 交
交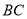 于点
于点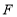 ,且
,且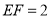 ,则
,则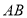 的长为__________.
的长为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)上题(2)中的面积最大的格点正方形边长为 (填有理数或无理数).
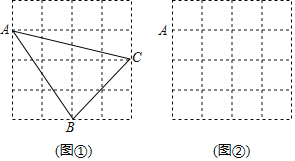
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中点
 ,
,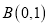 ,以
,以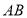 为顶点在第一象限内作正方形
为顶点在第一象限内作正方形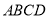 .反比例函数
.反比例函数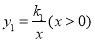 、
、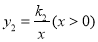 分别经过
分别经过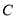 、
、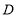 两点(1)如图2,过
两点(1)如图2,过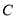 、
、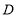 两点分别作
两点分别作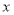 、
、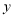 轴的平行线得矩形
轴的平行线得矩形 ,现将点
,现将点 沿
沿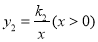 的图象向右运动,矩形
的图象向右运动,矩形 随之平移;
随之平移;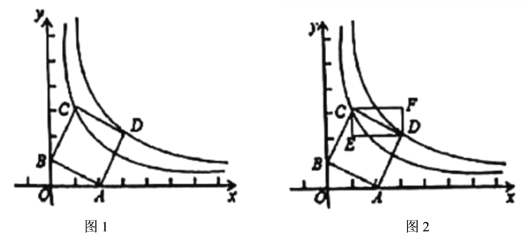
①试求当点
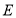 落在
落在 的图象上时点
的图象上时点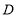 的坐标_____________.
的坐标_____________.②设平移后点
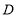 的横坐标为
的横坐标为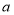 ,矩形的边
,矩形的边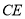 与
与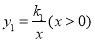 ,
,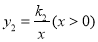 的图象均无公共点,请直接写出
的图象均无公共点,请直接写出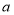 的取值范围____________.
的取值范围____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在边长为
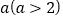 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。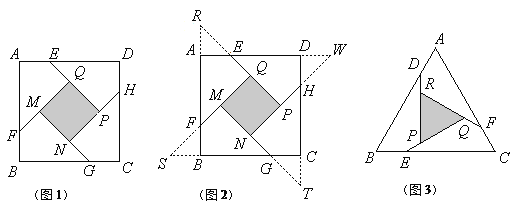
小明发现:分别延长QE、MF、NG、PH交FA、GB、HC、ED的延长线于点R、S、T、W可得△RQF、△SMG、△TNH、△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D、E、F作BC、AC、AB的垂线,得到等边△RPQ,若
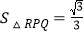 ,则AD的长为__________.
,则AD的长为__________.
相关试题

