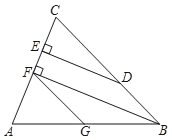
【题目】已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
参考答案:
【答案】BC,同位角相等,两直线平行,两直线平行,内错角相等,等量代换,同旁内角互补,两直线平行,∠DEA,垂直的定义.
【解析】
先根据![]() 得出
得出![]() ,故可得出
,故可得出![]() ,由
,由![]() 可得出
可得出![]() ,据此可得出结论.
,据此可得出结论.
解:∵∠AGF=∠ABC(已知)
∴FG∥BC(同位角相等,两直线平行)
∴∠BFG=∠FBC(两直线平行,内错角相等)
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°(等量代换)
∴BF∥DE(同旁内角互补,两直线平行)
∴∠BFA=∠DEA(两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°(垂直的定义)
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义).
故答案为:![]() ,同位角相等,两直线平行,两直线平行,内错角相等,等量代换,同旁内角互补,两直线平行,
,同位角相等,两直线平行,两直线平行,内错角相等,等量代换,同旁内角互补,两直线平行,![]() ,垂直的定义.
,垂直的定义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组条件中,能够判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
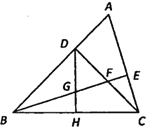
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线,在△ABC中,∠B=30°,AD和 DE是△ABC的三分线,点D在 BC 边上,点E在 AC边上,且AD=BD,DE=CE,请写出∠C所有可能的度数________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
-
科目: 来源: 题型:
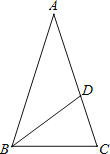
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
相关试题

