【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
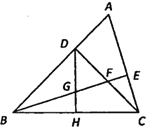
参考答案:
【答案】6
【解析】
求出 BG=GC,求出∠EGC=∠ECG,推出 CE=GE,进而利用等腰三角形的性质和全等三角形的判定和性质解答即可.
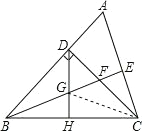
解:连接 CG,
∵BD=DC,H 为 BC 中点,
∴DH 为 BC 垂直平分线,
∴BG=CG,
∴∠ABE=∠CBE=∠GCB,
∵∠ABC=45°,∠ABE=∠CBE,
∴∠EGC=∠CBE+∠GCB=45°,
∵∠GEC=90°,
∴∠ECG=45°=∠EGC,
∴GE=CE=3.
∵BE 平分∠ABC,且 BE⊥AC 于点 E,
∴AE=EC=3,
∴AC=6,
∵CD⊥AB,
∴∠CDB=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠DBC,
∴BD=DC,
在△BDF 和△CEF 中,
∵∠BDC=∠BEC=90°,∠DFB=∠EFC,
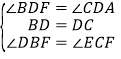 ∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴△BDF≌△CDA(ASA),
∴BF=AC=6; 故答案为:6;
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题
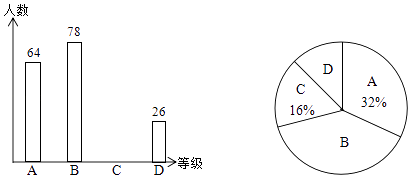
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t;5辆大货车与6辆小货车一次可以运货35t
(1)每辆大货车和每辆小货车一次各可以运货多少?
(2)现在租用这两种火车共10辆,要求一次运输货物不低于30t,则大货车至少租几辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,若AB=16cm,AC=12cm,BC=20cm.点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,如果点P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,请用含t的代数式表示,①当点Q在AC上时,CQ= ;②当点Q在AB上时,AQ= ;
③当点P在AB上时,BP= ;④当点P在BC上时,BP= .
(2)如图2,若点P在线段AB上运动,点Q在线段CA上运动,当QA=AP时,试求出t的值.
(3)如图3,当P点到达C点时,P、Q两点都停止运动,当AQ=BP时,试求出t的值.
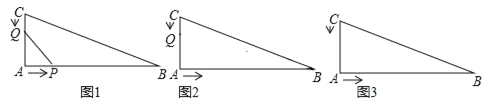
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切
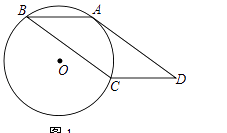
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=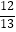 ,求tan∠D
,求tan∠D 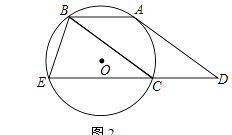
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线,在△ABC中,∠B=30°,AD和 DE是△ABC的三分线,点D在 BC 边上,点E在 AC边上,且AD=BD,DE=CE,请写出∠C所有可能的度数________.
相关试题

