【题目】列方程解应用题:为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车.他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?
参考答案:
【答案】小李骑电动车的速度为每小时![]() 千米,则自驾车的速度为每小时20千米
千米,则自驾车的速度为每小时20千米
【解析】
首先设小李骑电动车的速度为每小时x千米,根据题意可得等量关系:骑电动车所用的时间-自驾车所用的时间=![]() ,根据等量关系,列出方程,再解即可.
,根据等量关系,列出方程,再解即可.
设小李骑电动车的速度为每小时x千米,则自驾车的速度为每小时1.5x千米,
根据题意列方程:![]()
解得x=![]() .
.
经检验:x=![]() 是方程的解,且符合题意 .
是方程的解,且符合题意 .
所以![]() = 20 .
= 20 .
答:小李骑电动车的速度为每小时![]() 千米,则自驾车的速度为每小时20千米.
千米,则自驾车的速度为每小时20千米.
-
科目: 来源: 题型:
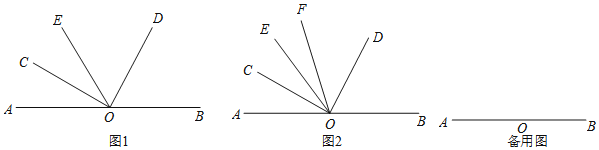
查看答案和解析>>【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题:
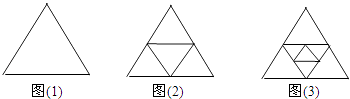
在第n个图形中有个三角形(用含n的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
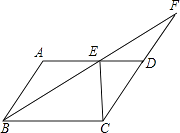
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D均在已知圆上,AD∥BC, AC平分∠BCD, 请找出图中与弦AD相等的线段,并加以证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=6,N为AB上一点,且AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是( )
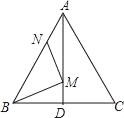
A. 8 B. 10 C.
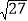 D. 2
D. 2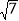
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


相关试题

