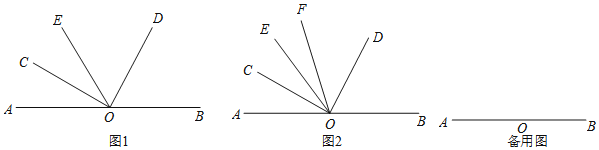
【题目】点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
参考答案:
【答案】(1)2;(2) 135°;(3)67.5°.
【解析】试题分析:
(1)由题意可得∠AOC=90°-∠BOD;∠AOE=![]() ∠AOD;∠AOD=180°-∠BOD;把上述三个关系式代入∠COE=∠AOE-∠AOC中化简即可得到∠COE=
∠AOD;∠AOD=180°-∠BOD;把上述三个关系式代入∠COE=∠AOE-∠AOC中化简即可得到∠COE=![]() ∠BOD,从而可得出∠BOD=2∠COE;
∠BOD,从而可得出∠BOD=2∠COE;
(2)由OC为∠AOE的角平分线,OF平分∠COD可得:∠AOC=∠COE,∠DOF=∠COF=45°;结合∠BOD+∠AOC=90°,∠EOC+∠FOB=∠EOC+∠FOD+∠BOD即可求得∠EOC+∠FOB的度数;
(3)如备用图,设∠EOF= ![]() ,则∠EOC=
,则∠EOC=![]() ,结合(2)可得∠AOE=2∠EOC=
,结合(2)可得∠AOE=2∠EOC=![]() ,∠COF=
,∠COF=![]() =45°,由此即可解得∠AOE=67.5°.
=45°,由此即可解得∠AOE=67.5°.
试题解析:
(1)∠BOD=2∠COE;理由如下:
∵∠COD=90°.
∴∠BOD+∠AOC=90°,
∵OE平分∠AOD,
∴∠AOE=∠DOE=![]() ∠AOD,
∠AOD,
又∵∠BOD=180°-∠AOD,
∴∠COE=∠AOE-∠AOC=![]() ∠AOD-(90°-∠BOD)=
∠AOD-(90°-∠BOD)=![]() (180°-∠BOD)-90°+∠BOD=
(180°-∠BOD)-90°+∠BOD=![]() ∠BOD,
∠BOD,
∴∠BOD=2∠COE;
(2)∵OC为∠AOE的角平分线,OF平分∠COD,
∴∠AOC=∠COE,∠COF=∠DOF=45°,
∴∠FOB+∠EOC=∠DOF+∠BOD+∠AOC=45°+90°=135°;
(3)如备用图:∵∠EOC=3∠EOF,
∴设∠EOF=x,则∠EOC=3x,
∴∠COF=4x,
∴结合(2)可得:∠AOE=2∠COE=6x,∠COF=4x=45°,
解得:x=11.25°,
∴∠AOE=6×11.25°=67.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】报社需要在40分钟内将一篇紧急宣传文稿输入电脑.已知独立完成此项任务,小王需要50分钟,小李只需要30分钟.小王独自输入了30分钟后,因为急于完成任务,请求小李帮助他(求助时间忽略不计),他们能在要求的时间内完成任务吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是半径为3的圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使
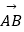 和
和 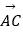 都经过圆心O,则阴影部分面积是。
都经过圆心O,则阴影部分面积是。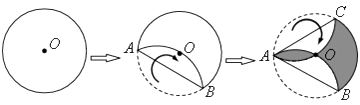
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为
 。
。
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形的中点得到图2;再分别连接图2中间的小三角形的中点,得到图3,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下面问题:
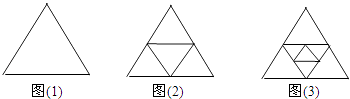
在第n个图形中有个三角形(用含n的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
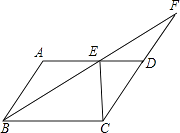
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车.他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?
相关试题

