【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,且
轴的正半轴上,且![]() .若抛物线经过
.若抛物线经过![]() 两点,且顶点在
两点,且顶点在![]() 边上,对称轴交
边上,对称轴交![]() 于点
于点![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() .
.
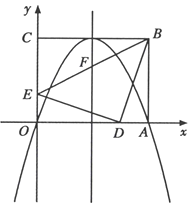
(1)求抛物线的解析式;
(2)猜想![]() 的形状并加以证明;
的形状并加以证明;
(3)点![]() 在对称轴右侧的抛物线上,点
在对称轴右侧的抛物线上,点![]() 在
在![]() 轴上,请问是否存在以点
轴上,请问是否存在以点![]() 为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点
为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣![]() x2+3x;(2)△EDB为等腰直角三角形,证明见解析;(3)存在.点M坐标为(
x2+3x;(2)△EDB为等腰直角三角形,证明见解析;(3)存在.点M坐标为(![]() ,2)或(
,2)或(![]() ,﹣2).
,﹣2).
【解析】
试题分析:(1)由条件可求得抛物线的顶点坐标及A点坐标,利用待定系数法可求得抛物线解析式;
(2)由B、D、E的坐标可分别求得DE、BD和BE的长,再利用勾股定理的逆定理可进行判断;
(3)由B、E的坐标可先求得直线BE的解析式,则可求得F点的坐标,当AF为边时,则有FM∥AN且FM=AN,则可求得M点的纵坐标,代入抛物线解析式可求得M点坐标;当AF为对角线时,由A、F的坐标可求得平行四边形的对称中心,可设出M点坐标,则可表示出N点坐标,再由N点在x轴上可得到关于M点坐标的方程,可求得M点坐标.
试题解析: (1)在矩形OABC中,OA=4,OC=3,∴A(4,0),C(0,3),
∵抛物线经过O、A两点,∴抛物线顶点坐标为(2,3),
∴可设抛物线解析式为y=a(x﹣2)2+3,
把A点坐标代入可得0=a(4﹣2)2+3,解得a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x﹣2)2+3,即y=﹣
(x﹣2)2+3,即y=﹣![]() x2+3x;
x2+3x;
(2)△EDB为等腰直角三角形.
证明如下:由(1)可知B(4,3),且D(3,0),E(0,1),
∴DE2=32+12=10,BD2=(4﹣3)2+32=10,BE2=42+(3﹣1)2=20,
∴DE2+BD2=BE2,且DE=BD,
∴△EDB为等腰直角三角形;
(3)存在.理由如下:
设直线BE解析式为y=kx+b,
把B、E坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BE解析式为y=![]() x+1,当x=2时,y=2,∴F(2,2),
x+1,当x=2时,y=2,∴F(2,2),
①当AF为平行四边形的一边时,则M到x轴的距离与F到x轴的距离相等,即M到x轴的距离为2,
∴点M的纵坐标为2或﹣2,
在y=﹣![]() x2+3x中,令y=2可得2=﹣
x2+3x中,令y=2可得2=﹣![]() x2+3x,解得x=
x2+3x,解得x=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∴x=![]() ,
,
∴M点坐标为(![]() ,2);
,2);
在y=﹣![]() x2+3x中,令y=﹣2可得﹣2=﹣
x2+3x中,令y=﹣2可得﹣2=﹣![]() x2+3x,解得x=
x2+3x,解得x=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∴x=![]() ,
,
∴M点坐标为(![]() ,﹣2);
,﹣2);
②当AF为平行四边形的对角线时,
∵A(4,0),F(2,2),
∴线段AF的中点为(3,1),即平行四边形的对称中心为(3,1),
设M(t,﹣![]() t2+3t),N(x,0),
t2+3t),N(x,0),
则﹣![]() t2+3t=2,解得t=
t2+3t=2,解得t=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∴t=![]() ,
,
∴M点坐标为(![]() ,2);
,2);
综上可知存在满足条件的点M,其坐标为(![]() ,2)或(
,2)或(![]() ,﹣2).
,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠A= 37°49',则∠A的补角为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式从左到右的变形中,是因式分解的是( )
A.x2﹣9+6x=(x+3)(x﹣3)+6x
B.6ab=2a3b
C.x2﹣8x+16=(x﹣4)2
D.(x+5)(x﹣2)=x2+3x﹣10 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
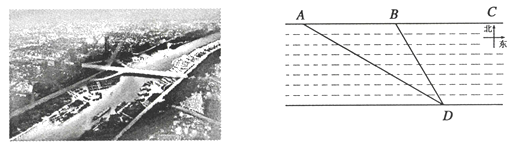
查看答案和解析>>【题目】如图,建设“幸福西宁”,打造“绿色发展样板城市”.美丽的湟水河宛如一条玉带穿城而过,已形成“水清、流畅、岸绿、景美”的生态环境新格局.在数学课外实践活动中,小亮在海湖新区自行车绿道北段
 上的
上的 两点分别对南岸的体育中心
两点分别对南岸的体育中心 进行测量,分别没得
进行测量,分别没得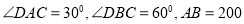 米,求体育中心
米,求体育中心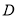 到湟水河北岸
到湟水河北岸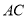 的距离约为多少米(精确到1米,
的距离约为多少米(精确到1米,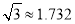 )?
)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE.
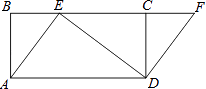
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
相关试题

