【题目】在平面直角坐标系中,给出如下定义:形如y=(x﹣m)(x﹣m+1)与y=(x﹣m)(x﹣m﹣1)的两个二次函数的图象叫做兄弟抛物线.
(1)试写出一对兄弟抛物线的解析式.
(2)若二次函数y=x2﹣x(图象如图)与y=x2﹣bx+2的图象是兄弟抛物线.
①求b的值.
②若直线y=k与这对兄弟抛物线有四个交点,从左往右依次为A,B,C,D四个点,若点B,点C为线段AD三等分点,求线段BC的长.

参考答案:
【答案】(1)y=x(x+1)与y=x(x﹣1);
(2)①b=3.②线段BC的长为1或![]() .
.
【解析】试题分析:(1)将m=0代入y=(x-m)(x-m+1)与y=(x-m)(x-m-1),即可得到一对兄弟抛物线;
(2)①y=x2-x=x(x-1).分两种情况讨论:
情况一:若y=x(x-1)是形如y=(x-m)(x-m+1),求出m=1,得到另一个函数解析式,进而得出b的值;
情况二:若y=x(x-1)是形如y=(x-m)(x-m-1),同理求解;
②根据平移的规律可知,y=x2-3x+2的图象可以看作是由y=x2-x的图象向右平移1个单位得到,分两种情况:如果k>0,则点A与点B是平移对应点,AB=1,再根据三等分点的定义即可求解;如果k<0,则点A与点C是平移对应点,AC=1,同理求解即可.
试题解析:(1)当m=0时,得到一对兄弟抛物线,
y=x(x+1)与y=x(x﹣1);
(2)①y=x2﹣x=x(x﹣1).
情况一:若y=x(x﹣1)是形如y=(x﹣m)(x﹣m+1),则m=1,则另一个函数为y=(x﹣1)(x﹣2),即y=x2﹣3x+2,b=3.
情况二:若y=x(x﹣1)是形如y=(x﹣m)(x﹣m﹣1),则m=0,则另一个函数为y=x(x﹣1),即y=x2﹣x,与已知矛盾.
②y=x2﹣3x+2的图象可以看作是由y=x2﹣x的图象向右平移1个单位得到,如图.
如果k>0,则点A与点B是平移对应点,AB=1,
∵点B,点C为线段AD三等分点,
∴AB=BC=CD=![]() AD=1,即BC=1;
AD=1,即BC=1;
如果k<0,则点A与点C是平移对应点,AC=1,
∵点B,点C为线段AD三等分点,
∴AB=BC=![]() AC=
AC=![]() ,即BC=
,即BC=![]() .
.
故线段BC的长为1或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】只用下列一种正多边形不能镶嵌成平面图案的是( )
A. 正三角形B. 正方形C. 正五边形D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】与正三角形组合在一起能铺满地面的另一种正多边形是____.(只要求写出一种即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)已知二次函数y=ax2+bx+c过点A(1,0),B(﹣3,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为6,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
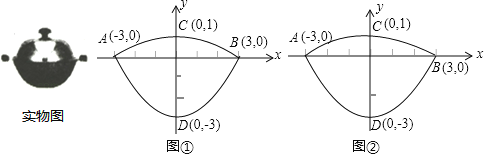
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm -
科目: 来源: 题型:
查看答案和解析>>【题目】幼儿园的小朋友打算选择一种形状、大小都相同的多边形塑料胶板铺地面.为了保证铺地时既无缝隙,又不重叠,请你告诉他们可以选择哪些形状的塑料胶板 (填三种).
相关试题

