【题目】(本题8分)已知二次函数y=ax2+bx+c过点A(1,0),B(﹣3,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为6,求点P的坐标.

参考答案:
【答案】(1)设抛物线的解析式为y=a(x1)(x+3),
(2)P(1+![]() ,3)或P(1
,3)或P(1![]() ,3)或(0,3)或P(2,3).
,3)或(0,3)或P(2,3).
【解析】试题分析:(1)由于已知了抛物线与x的两交点坐标,则可设交点式y=a(x+1)(x-3),然后把C点坐标代入计算出a即可.
(2)首先算出AB的长,再设P(m,n),根据△ABP的面积为6可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标.
试题解析:(1)设抛物线的解析式为y=a(x1)(x+3),
把C(0,3)代入得a×(1)×3=3,
解得a=1,
所以这个二次函数的解析式为y=(x1)(x+3)=x2+2x3.
(2)∵A(1,0),B(3,0),
∴AB=4,
设P(m,n),
∵△ABP的面积为6,
∴![]() AB|n|=6,
AB|n|=6,
解得:n=±3,
当n=3时,m2+2m3=3,
解得:m=1+7√或17√,
∴P(1+![]() ,3)或P(1
,3)或P(1![]() ,3);
,3);
当n=3时,m2+2m3=5,
解得m=0或m=2,
∴P(0,3)或P(2,3);
故P(1+![]() ,3)或P(1
,3)或P(1![]() ,3)或(0,3)或P(2,3).
,3)或(0,3)或P(2,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+kx+16=0有两个相等的实数根,则k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】只用下列一种正多边形不能镶嵌成平面图案的是( )
A. 正三角形B. 正方形C. 正五边形D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】与正三角形组合在一起能铺满地面的另一种正多边形是____.(只要求写出一种即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,给出如下定义:形如y=(x﹣m)(x﹣m+1)与y=(x﹣m)(x﹣m﹣1)的两个二次函数的图象叫做兄弟抛物线.
(1)试写出一对兄弟抛物线的解析式.
(2)若二次函数y=x2﹣x(图象如图)与y=x2﹣bx+2的图象是兄弟抛物线.
①求b的值.
②若直线y=k与这对兄弟抛物线有四个交点,从左往右依次为A,B,C,D四个点,若点B,点C为线段AD三等分点,求线段BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
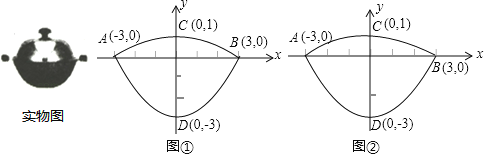
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm
相关试题

