【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
参考答案:
【答案】C
【解析】试题分析:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
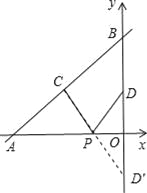
直线y=![]() x+4与x轴、y轴的交点坐标为A(﹣6,0)和点B(0,4),因点C、D分别为线段AB、OB的中点,可得点C(﹣3,2),点D(0,2).再由点D′和点D关于x轴对称,可知点D′的坐标为(0,﹣2).设直线CD′的解析式为y=kx+b,直线CD′过点C(﹣3,2),D′(0,﹣2),所以
x+4与x轴、y轴的交点坐标为A(﹣6,0)和点B(0,4),因点C、D分别为线段AB、OB的中点,可得点C(﹣3,2),点D(0,2).再由点D′和点D关于x轴对称,可知点D′的坐标为(0,﹣2).设直线CD′的解析式为y=kx+b,直线CD′过点C(﹣3,2),D′(0,﹣2),所以![]() ,解得:
,解得: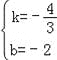 ,即可得直线CD′的解析式为y=﹣
,即可得直线CD′的解析式为y=﹣![]() x﹣2.令y=﹣
x﹣2.令y=﹣![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣![]() ,所以点P的坐标为(﹣
,所以点P的坐标为(﹣![]() ,0).故答案选C.
,0).故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据1,a,3,6,7,它的平均数是4,这组数据的中位数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(1,a)与Q(b,2)关于x轴对称,则代数式(a+b)2017的值为( )
A.﹣1
B.1
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正n边形的每个外角均为40°,则n=( )
A. 6 B. 7 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的一个内角为140°,则该正多边形的边数为( )
A. 9 B. 8 C. 7 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰三角形ABC中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( )

A.4 B.
 C.3
C.3 D.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若点P(a,b)在函数y=
 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y= 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2,  )在函数y=
)在函数y=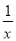 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+  称为函数y=
称为函数y= 的一个“派生函数”.现给出以下两个命题:
的一个“派生函数”.现给出以下两个命题:(1)存在函数y=
 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧(2)函数y=
 的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”的图象都经过同一点,下列判断正确的是( )A. 命题(1)与命题(2)都是真命题
B. 命题(1)与命题(2)都是假命题
C. 命题(1)是假命题,命题(2)是真命题
D. 命题(1)是真命题,命题(2)是假命题
相关试题

