Question

【题目】如图，已知四边形BCDE为平行四边形，点A在BE的延长线上且AE=EB．连接EC，AC，AD．

（1）求证：△AED≌△EBC．
（2）若∠ACB=90°，则四边形AECD是什么特殊四边形？请说明理由．

Answer 1

【答案】
（1）证明：∵四边形BCDE是平行四边形，

∴ED∥BC，DE=BC，

∴∠AED=∠B，

在△AED和△EBC中，

，

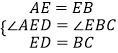∴△AED≌△EBC

（2）解：结论：四边形AECD是菱形．

理由：∵四边形BCDE是平行四边形，

∴AB∥CD，BE=CD，

∵AE=BE，

∴AE=CD，AE∥CD，

∴四边形AECD是平行四边形，

∵∠ACB=90°，

∴AC⊥BC，∵BC∥DE，

∴AC⊥DE，

∴四边形AECD是菱形．

【解析】（1）根据平行四边形的性质得出ED∥BC，DE=BC，进而得出∠AED=∠B，然后利用SAS判断出△AED≌△EBC；
（2）结论：四边形AECD是菱形．利用平行四边形的性质得出AB∥CD，BE=CD，进而判断出四边形AECD是平行四边形，然后根据平行线的性质得出AC⊥DE，从而得出四边形AECD是菱形．
【考点精析】本题主要考查了平行线的性质和平行四边形的性质的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．