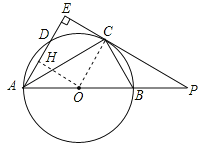
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
参考答案:
【答案】(1)证明见试题解析;(2)AB=3PB,理由见试题解析;(3)5.
【解析】
试题分析:(1)首先连接OC,由PE是⊙O的切线,AE和过点C的切线互相垂直,可证得OC∥AE,又由OA=OC,易证得∠DAC=∠OAC,即可得AC平分∠BAD;
(2)由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;
(3)首先过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,即可得AE=
,四边形OCEH是矩形,即可得AE=![]() +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
+OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
试题解析:(1)连接OC,∵PE是⊙O的切线,∴OC⊥PE,∵AE⊥PE,∴OC∥AE,∴∠DAC=∠OCA,∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OAC,∴AC平分∠BAD;
(2)线段PB,AB之间的数量关系为:AB=3PB.理由:
∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,∵OB=OC,∴∠OCB=∠ABC,∵∠PCB+∠OCB=90°,∴∠PCB=∠PAC,∵∠P是公共角,∴△PCB∽△PAC,∴![]() ,∴
,∴![]() =PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
=PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
(3)过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,∴OC=HE,∴AE=
,四边形OCEH是矩形,∴OC=HE,∴AE=![]() +OC,∵OC∥AE,∴△PCO∽△PEA,∴
+OC,∵OC∥AE,∴△PCO∽△PEA,∴![]() ,∵AB=3PB,AB=2OB,∴OB=
,∵AB=3PB,AB=2OB,∴OB=![]() PB,∴
PB,∴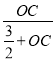 =
=![]() =
=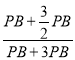 ,∴OC=
,∴OC=![]() ,∴AB=5,∵△PBC∽△PCA,∴
,∴AB=5,∵△PBC∽△PCA,∴![]() ,∴AC=2BC,在Rt△ABC中,
,∴AC=2BC,在Rt△ABC中,![]() ,∴
,∴![]() ,∴BC=
,∴BC=![]() ,∴AC=
,∴AC=![]() ,∴S△ABC=
,∴S△ABC=![]() ACBC=5.
ACBC=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中
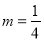 ,n=-1.”小强不小心把
,n=-1.”小强不小心把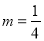 错抄成了
错抄成了 ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】王老师把数学测验成绩高于班级平均分8分的记为+8分,则低于平均分5分的可记为____分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
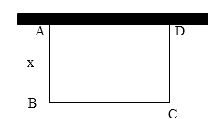
(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=-x2+2x+n图象的顶点坐标是(m,1),则m-n的值为( )
A.1B.0C.1D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口约为44亿人,数据44亿用科学记数法表示为( )
A. 44×108 B. 4.4×109 C. 4.4×108 D. 44×1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程ax2+3x=ax+2是一元二次方程,那么( )
A.a≠0B.a≠1C.a≠2D.a≠3
相关试题

