【题目】若二次函数y=-![]() x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0).
x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0).
(1)求这个二次函数的关系式;
(2)如果要通过适当的平移,使得这个函数的图象与x轴只有一个交点,那么应该怎样平移?向右还是向左?或者是向上还是向下?应该平移向个单位?
参考答案:
【答案】(1)y=![]() ;(2)应向下平移2个单位.
;(2)应向下平移2个单位.
【解析】本题考查二次函数平移的基本性质及函数的顶点坐标,运用待定系数法求抛物线的解析式
(1)由题意二次函数y=-![]() x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0),把点代入二次函数的解析式,根据待定系数法求出函数的解析式.
x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0),把点代入二次函数的解析式,根据待定系数法求出函数的解析式.
(2)把(1)求得的解析式化为顶点式,再根据平移的性质解答.
(1)∵y=![]() x2+bx+c,把A(-5,0),B(-1,0)代入上式,得
x2+bx+c,把A(-5,0),B(-1,0)代入上式,得
∴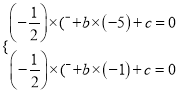 ,
, ,
,
∴y=![]() .
.
(2)∵y=![]() =
=![]()
∴顶点坐标为(-3,2),
∴欲使函数的图象与x轴只有一个交点,应向下平移2个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市测一周PM2.5的月均值(单位:微克/立方米)如下:50,40,73,50,37,50,40,这组数据的中位数和众数分别是( )
A. 50和50B. 50和40C. 40和50D. 40和40
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线
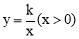 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=
 x2+5x+1000,Q=-
x2+5x+1000,Q=- +45.
+45.(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】按一定规律排列的一列数:21 , 22 , 23 , 25 , 28 , 213 , …,若x,y,z表示这列数中的连续三个数,则x、y、z满足的关系式是( )
A.x+y=z
B.xy=z
C.x+y>z
D.xy>z -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(2,4)向右平移2个单位长度,再向上平移1个单位长度得到点B,则点B的坐标为( )
A. ( 3 , 6 )B. ( 0 , 5 )C. ( 4 , 5 )D. ( 4 , 3 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧
 围成的弓形面积.
围成的弓形面积.
相关试题

