【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.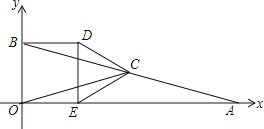
(1)线段OC的长为;
(2)求证:△CBD≌△COE;
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1 , 其中点O,B,D,E的对应点分别为点O1 , B1 , D1 , E1 , 连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S= ![]() 时,请直接写出a的值.
时,请直接写出a的值.
参考答案:
【答案】
(1)![]()
(2)
证明:∵∠AOB=90°,点C是AB的中点,
∴OC=BC= ![]() AB,
AB,
∴∠CBO=∠COB,
∵四边形OBDE是正方形,
∴BD=OE,∠DBO=∠EOB=90°,
∴∠CBD=∠COE,
在△CBD和△COE中,
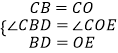 ,
,
∴△CBD≌△COE(SAS)
(3)
解:①解:过点C作CH⊥D1E1于点H,
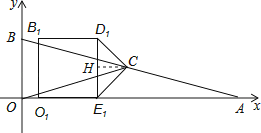
∵C是AB边的中点,
∴点C的坐标为:(2, ![]() )
)
∵点E的坐标为(a,0),1<a<2,
∴CH=2﹣a,
∴S= ![]() D1E1CH=
D1E1CH= ![]() ×1×(2﹣a)=﹣
×1×(2﹣a)=﹣ ![]() a+1;
a+1;
②当1<a<2时,S=﹣ ![]() a+1=
a+1= ![]() ,
,
解得:a= ![]() ;
;
当a>2时,同理:CH=a﹣2,
∴S= ![]() D1E1CH=
D1E1CH= ![]() ×1×(a﹣2)=
×1×(a﹣2)= ![]() a﹣1,
a﹣1,
∴S= ![]() a﹣1=
a﹣1= ![]() ,
,
解得:a= ![]() ,
,
综上可得:当S= ![]() 时,a=
时,a= ![]() 或
或 ![]() .
.
【解析】解:(1)∵点A的坐标为(4,0),点B的坐标为(0,1),
∴OA=4,OB=1,
∵∠AOB=90°,
∴AB= ![]() =
= ![]() ,
,
∵点C为边AB的中点,
∴OC= ![]() AB=
AB= ![]() ;故答案为:
;故答案为: ![]() .
.
(1)由点A的坐标为(4,0),点B的坐标为(0,1),利用勾股定理即可求得AB的长,然后由点C为边AB的中点,根据直角三角形斜边的中线等于斜边的一半,可求得线段OC的长;(2)由四边形OBDE是正方形,直角三角形斜边的中线等于斜边的一半,易得BD=OE,BC=OC,∠CBD=∠COE,即可证得:△CBD≌△COE;(3)①首先根据题意画出图形,然后过点C作CH⊥D1E1于点H,可求得△CD1E1的高与底,继而求得答案;
②分别从1<a<2与a>2去分析求解即可求得答案. 此题属于四边形的综合题.考查了正方形的性质、直角三角形的性质、勾股定理、全等三角形的判定与性质以及三角形面积问题.注意掌握辅助线的作法,注意掌握分类讨论思想的应用是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
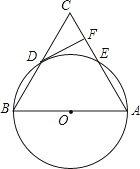
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求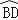 的长(结果保留π).
的长(结果保留π). -
科目: 来源: 题型:
查看答案和解析>>【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,P是CD边上一点,DF⊥AP,BE⊥AP.
求证:AE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.

(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
相关试题

