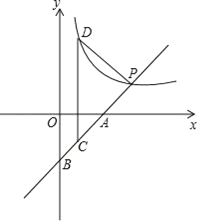
【题目】如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
参考答案:
【答案】(1)y=![]() (2)当C(2,-2)时,△CDP为等腰直角三角形
(2)当C(2,-2)时,△CDP为等腰直角三角形
【解析】试题分析:(1)过P作PE⊥x轴于点E,求出点P的坐标,进而求出反比例函数的解析式;
(2)首先求出直线AB的解析式,然后设C(m,m-4),则D(m, ![]() ),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
),过P作PF⊥CD于F.则F(m,2),则F(m,2),根据DF=CF列出m的方程求出m即可.
试题解析:(1)过P作PE⊥x轴于点E,∵tan∠BAO=1,∴∠BAO=45°,
∴∠BAO=∠ABO=∠PAE=45°
∵点P的纵坐标为2,∴PE=AE=2,∵A(4,0),∴P(6,2)
把点P代人y=![]() 得k=12.∴反比例函数的解析式为y=
得k=12.∴反比例函数的解析式为y=![]()
(2)设直线AB的解析式为y=kx+b且过A(4,0),P(6,2)
![]() ,解得
,解得![]() ,∴y=x-4
,∴y=x-4
要使△CDP是等腰直角三角形,只能∠DPC=90°,
设C(m,m-4),则D(m, ![]() ).过P作PF⊥CD于F.则F(m,2),
).过P作PF⊥CD于F.则F(m,2),
∴PD=PC,PF⊥CD,∴DF=CF,∴![]() -2=2-(m-4),
-2=2-(m-4),
∴m2-8m+12=0,(m-2)(m-6)=0,∴m1=2,m2=6(不合题意,舍去),
∴当C(2,-2)时,△CDP为等腰直角三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,﹣2)关于y轴的对称点是 , 关于原点的对称点是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高全民健康意识,2018年11月25日共青团宝应县委继续组织了一次万人参加的“全民健康行”毅行活动,这次毅行活动的行程约为20000m,将20000m用科学记数法表示为______m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2
 ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3xy2)2+(﹣4xy3)(﹣xy)=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数
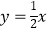 的图象相交于点(2,a).
的图象相交于点(2,a).
(1)求a的值.
(2)求一次函数y=kx+b的表达式.
(3)在同一坐标系中,画出这两个函数的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)

相关试题

