【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
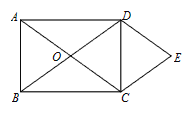
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
参考答案:
【答案】(1)四边形OCED是菱形.(2)24.
【解析】
试题分析:(1)首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.
(2)连接OE,通过证四边形BOEC是平行四边形,得OE=BC;根据菱形的面积是对角线乘积的一半,可求得四边形ODEC的面积.
试题解析:(1)四边形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连接OE.由菱形OCED得:CD⊥OE,

又∵BC⊥CD,
∴OE∥BC(在同一平面内,垂直于同一条直线的两直线平行),
又∵CE∥BD,
∴四边形BCEO是平行四边形;
∴OE=BC=8
∴S四边形OCED=![]() OECD=
OECD=![]() ×8×6=24.
×8×6=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过原点的直线
 和
和 与反比例函数
与反比例函数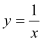 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.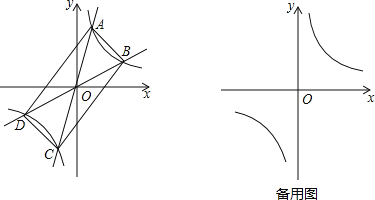
(1)四边形ABCD一定是 形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由;
(3)设P(
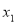 ,
, ),Q(
),Q(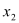 ,
, )(x2 >x1 >0)是函数
)(x2 >x1 >0)是函数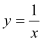 图象上的任意两点,
图象上的任意两点, ,
, ,试判断
,试判断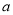 ,
,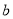 的大小关系,并说明理由.
的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
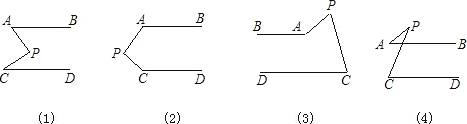
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙ 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。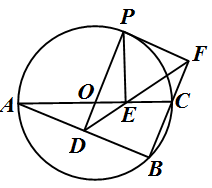
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙
 的切线。
的切线。 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意三角形的高,下列说法不正确的是( )
A. 直角三角形只有一条高
B. 锐角三角形有三条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有四根木棒,长度分别为4cm,6cm,8cm,10cm,从中任取三根木棒,能组成三角形的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:m2m3= .
相关试题

