【题目】如图,过原点的直线![]() 和
和![]() 与反比例函数
与反比例函数![]() 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
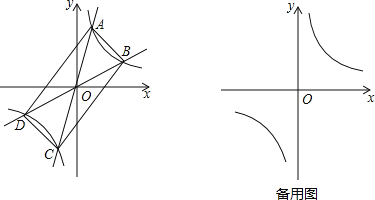
(1)四边形ABCD一定是 形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由;
(3)设P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() )(x2 >x1 >0)是函数
)(x2 >x1 >0)是函数![]() 图象上的任意两点,
图象上的任意两点,![]() ,
,![]() ,试判断
,试判断![]() ,
,![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
参考答案:
【答案】(1)平行;(2)k1k2=1;(3)a>b.
【解析】
试题分析:(1)由直线y=k1x和y=k2x与反比例函数y=![]() 的图象关于原点对称,即可得到结论.
的图象关于原点对称,即可得到结论.
(2)联立方程求得A、B点的坐标,然后根据OA=OB,依据勾股定理得出 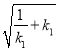 =
= ,两边平分得
,两边平分得![]() =
=![]() ,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可求得;
,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可求得;
(3)由P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=![]() 图象上的任意两点,得到y1=
图象上的任意两点,得到y1=![]() ,y2=
,y2=![]() ,求出a=
,求出a=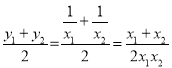 ,得到a-b=
,得到a-b=![]() =
= =
=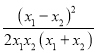 >0,即可得到结果.
>0,即可得到结果.
试题解析:(1)∵直线y=k1x和y=k2x与反比例函数y=![]() 的图象关于原点对称,
的图象关于原点对称,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形;
(2)解:∵正比例函数y=k1x(k1>0)与反比例函数y=![]() 的图象在第一象限相交于A,
的图象在第一象限相交于A,
∴k1x=![]() ,解得x=
,解得x=![]() (因为交于第一象限,所以负根舍去,只保留正根)
(因为交于第一象限,所以负根舍去,只保留正根)
将x=![]() 代入y=k1x得y=
代入y=k1x得y=![]() ,
,
故A点的坐标为(![]() ,
,![]() )同理则B点坐标为(
)同理则B点坐标为(![]() ,
,![]() ),
),
又∵OA=OB,
∴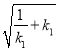 =
= ,两边平方得:
,两边平方得:![]() =
=![]() ,
,
整理后得(k1-k2)(k1k2-1)=0,
∵k1≠k2,
所以k1k2-1=0,即k1k2=1;
(3)∵P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=![]() 图象上的任意两点,
图象上的任意两点,
∴y1=![]() ,y2=
,y2=![]() ,
,
∴a=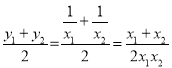 ,
,
∴a-b=![]() =
= =
=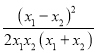 ,
,
∵x2>x1>0,
∴(x1-x2)2>0,x1x2>0,(x1+x2)>0,
∴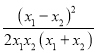 >0,
>0,
∴a-b>0,
∴a>b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a﹣3|+(b+3)2=0,则a2+2ab+b2的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长是0.9米,宽是b米,这个长方形的面积是0.9b米.请你再赋予0.9b一个含义 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=
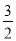 x-3与反比例函数
x-3与反比例函数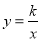 的图象相交于点A
的图象相交于点A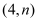 ,与x轴相交于点B.
,与x轴相交于点B.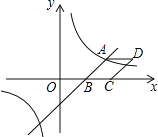
(1)填空:
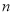 的值为 ,
的值为 ,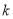 的值为 ;
的值为 ;(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数
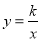 的图象,当
的图象,当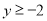 时,请直接写出自变量
时,请直接写出自变量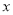 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
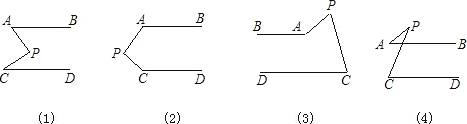
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙ 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。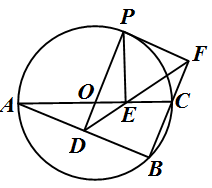
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙
 的切线。
的切线。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
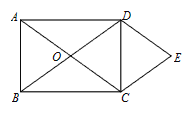
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
相关试题

