【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论中不正确的是( )
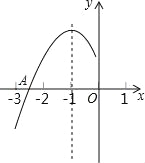
A.4ac﹣b2<0
B.2a﹣b=0
C.a+b+c<0
D.点(x1,y1)、(x2,y2)在抛物线上,若x1<x2,则y1<y2
参考答案:
【答案】D
【解析】
试题分析:根据函数与x中轴的交点的个数,以及对称轴的解析式,函数值的符号的确定即可作出判断.
A、函数与x轴有两个交点,则b2﹣4ac>0,即4ac﹣b2<0,故本选项正确;B、函数的对称轴是x=﹣1,即﹣![]() =﹣1,则b=2a,2a﹣b=0,故本选项正确;C、当x=1时,函数对应的点在x轴下方,则a+b+c<0,则本选项正确;D、因为不知道两点在对称轴的那侧,所以y1和y2的大小无法判断,则本选项错误.
=﹣1,则b=2a,2a﹣b=0,故本选项正确;C、当x=1时,函数对应的点在x轴下方,则a+b+c<0,则本选项正确;D、因为不知道两点在对称轴的那侧,所以y1和y2的大小无法判断,则本选项错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若-3xy2m与5x2n-3y8的和是单项式,则m、n的值分别是( )
A. m=2,n=2 B. m=4,n=1 C. m=4,n=2 D. m=2,n=3
-
科目: 来源: 题型:
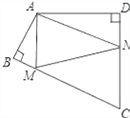
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳沙井某服装厂2017年销售额为8亿元,受中美贸易战影响,估计2019年销售额降为5.12亿元,设平均每年下降的百分比为x,可列方程为( )
A.8(1﹣x)=5.12B.8(1+x)2=5.12
C.8(1﹣x)2=5.12D.5.12(1+x)2=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AE平分∠BAD交BC于点E,CE=1,∠CAE=15°,则BE等于
相关试题

