【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90 ,得Rt△BDO,点B坐标为(0,-3),点C坐标为(0, ![]() ),,抛物线y=-
),,抛物线y=-![]() x2+bx+c经过点A和点C
x2+bx+c经过点A和点C
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?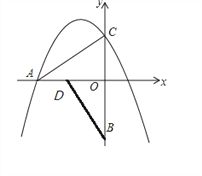
参考答案:
【答案】(1)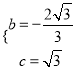 (2)存在,有2个Q点,坐标分别为:(—1,
(2)存在,有2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() )(3)当t=2或
)(3)当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形.
+1秒时,以M、P、O、C为顶点得四边形是平行四边形.
【解析】试题分析:(1)先由旋转得出点A的坐标为(—3,0),直接利用待定系数法求出抛物线解析式得出即可;
(2)利用当AQ=AC=![]() ,以及当AC=Q1C时,分别得出符合题意的答案即可;
,以及当AC=Q1C时,分别得出符合题意的答案即可;
(3)利用平行四边形的性质首先得出BC的长,进而表示出线段ME的长,进而求出答案.
(1) 由旋转知:OA=OB=3
∴A(—3,0)
由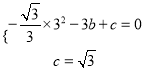 ,∴
,∴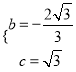 ……4分
……4分
(2)由(1)得y=-![]() x2+bx+c=-
x2+bx+c=-![]() x2
x2![]() x+
x+![]() =-
=-![]() x+1)2
x+1)2![]() ,即抛物线的对称轴为直线x=-1,
,即抛物线的对称轴为直线x=-1,
如图
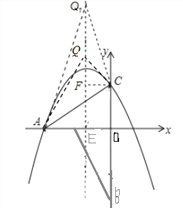
①当AC=AQ时,直线x=-1和x轴交于E点,AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,AE=2,∴QE=
,AE=2,∴QE=![]() ,故Q的坐标为:(-1,
,故Q的坐标为:(-1, ![]() );
);
②当AC=Q1C时,过点C作CF⊥直线x=-1,于一点F,则FC=1,
∵AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,∴Q1C=
,∴Q1C=![]() ,∴FQ1=
,∴FQ1=![]() ,故Q1的坐标为:(-1,
,故Q1的坐标为:(-1, ![]() );
);
所以存在2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() ).
).
(3)∵OC=![]() ,当 M、P、O、C为顶点得四边形是平行四边形时,PM=
,当 M、P、O、C为顶点得四边形是平行四边形时,PM=![]()
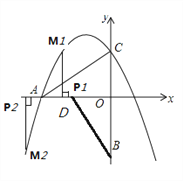
∴M点的纵坐标为![]() 或-
或-![]() .
.
由![]()
解之,x=-2或0
由 ![]()
解之,x=-1+![]() 或-1-
或-1-![]()
结合条件及图形分析得:OP=2或![]() +1
+1
∴当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形。
+1秒时,以M、P、O、C为顶点得四边形是平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AD>AB.

(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取?最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取?最小值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24.请写出运算式.(只需写出一种)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AC=BC,∠A=80°,则∠B=°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,1,5,0这四个数中,最大的数是( )
A.﹣2
B.1
C.5
D.0 -
科目: 来源: 题型:
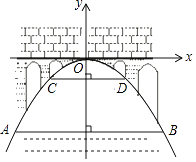
查看答案和解析>>【题目】如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
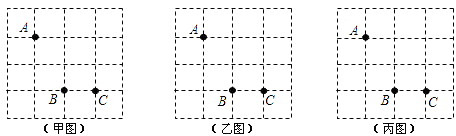
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
相关试题

