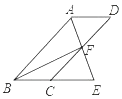
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:DC=BE;
(2)连接BF,若BF⊥AE,求证:△ADF≌△ECF.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE,从而得出BE=CD;
(2)先证明AF=EF,由AAS证明△ADF≌△ECF;
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD;
(2)证明:∵AB=BE,BF⊥AE,
∴AF=EF.
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,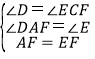 ,
,
∴△ADF≌△ECF(AAS),
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.

-
科目: 来源: 题型:
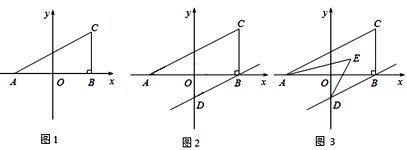
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足
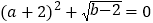 ,过C作
,过C作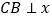 轴于B,
轴于B,(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,若存在,求出点P坐标,若不存在,试说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,图3,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上高,若AD=16,CD=12,BD=9.
(1)求△ABC的周长;
(2)判断△ABC的形状并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
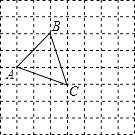
(1)格点△ABC的面积为;
(2)画出格点△ABC绕点C顺时针旋转90°后的△A1B1C1 , 并求出在旋转过程中,点B所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
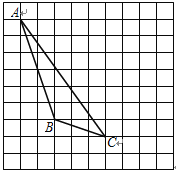
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
相关试题

