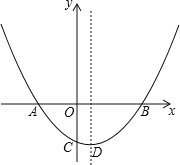
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)若点M为抛物线第四象限内一点,连接BC、CM、BM,求当△BCM的面积最大时点M的坐标.
参考答案:
【答案】(1)抛物线解析式为y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,抛物线的顶点坐标为(
,抛物线的顶点坐标为(![]() ,﹣
,﹣![]() ),(3)点M的坐标为(1,-1).
),(3)点M的坐标为(1,-1).
【解析】试题分析:(1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可.
(3)作出辅助线,利用tan∠MDN=2或![]() ,建立关于点N的横坐标的方程,求出即可.
,建立关于点N的横坐标的方程,求出即可.
试题解析:(1)∵抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,
∴![]()
∴ ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣1=
x﹣1=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴抛物线的顶点坐标为(![]() ,﹣
,﹣![]() ),
),
(2)如图1,
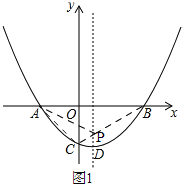
连接BC与抛物线对称轴的交点就是点P,连接AC,AP,
∵点A,B关于抛物线对称轴对称,
∴PA=PB,
∵B(2,0),C(0,﹣1),
∴直线BC解析式为y=![]() x﹣1,
x﹣1,
∵点P在抛物线对称轴上,
∴点P的横坐标为![]() ,
,
∴点P的纵坐标为﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
(3)设M(x, ![]() ),过点M作x轴的垂线交BC于点N,则点N(x,
),过点M作x轴的垂线交BC于点N,则点N(x, ![]() )
)
∴![]() =
=![]() =
=![]()
故当x=1时,S△BMC面积最大,此时![]() ,
,
所以当△BCM的面积最大时点M的坐标为(1,-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形ABCD旋转到平行四边形A′B′C′D′的位置,下列结论错误的是( )
A. AB=A′B′ B. AB∥A′B′ C. ∠A=∠A′ D. △ABC≌△A′B′C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?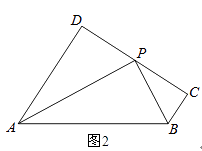
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3时,下列不等式成立的是( )
A. x+2<6 B. x-1<2
C. 2x-1<0 D. 2-x>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在投针试验中,当平行线空隙a为定值时,针的长度L越大则针与平行线相交的概率越_____;当L为定值时,a越大则针与平行线相交的概率越_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.
相关试题

